Hallo Gengs.. apa kabar? Pada kesempatan kali ini kita akan berlatih mengerjakan soal tentang sistem pertidaksamaan linear. Sebelum berlatih mengerjakan soal, ada baiknya Gengs pelajari terlebih dahulu materinya. Nahhh setelah kita kuasai materinya, mari kita latihan mengerjakan soal-soal untuk mengukur pemahaman kita.
Contoh 1
Perhatikan pertidaksamaan berikut:
4x+5y<20
Dari pertidaksamaan tersebut, gambar dan arsirlah daerah penyelesaiannya pada bidang koordinat cartesius kuadran 1.
Jawaban:
Yang perlu kita garis bawahi yaitu KUADRAN 1
Langkah 1
Ganti tanda pertidaksamaan menjadi persamaan:
4x+5y<20
4x+5y=20
Saat x=0 maka
4(0)+5y=20
5y=20
y=4
titik potong : (0,4)
saat y=0 maka
4x+5(0)=20
4x=20
x=5
Titik potongnya yaitu (5,0)
Langkah 2
Grafik berdasarkan titik (0,4) dan (5,0) yaitu
Langkah 3
Ambil titik uji untuk mendapatkan daerah penyelesaian dan pertidaksamaan.
Misalnya: (0,0)
4x+5y<20
4(0)+5(0)<20
0˂20 [BENAR]
Langkah 4
Grafik daerah penyelesaiannya
Karena pada langkah 40<20 [benar] maka daerah penyelesaiannya akan ada di sebelah kiri garis. Seperti gambar berikut:
Contoh 2
Tentukan daerah penyelesaian sistem pertidaksamaan linear berikut pada bidang koordinat cartesius!
5x+3y≤15
2x+5y≥10
x≥0
y≥0
Jawaban:
Langkah 1
Ubah pertidaksamaan 5x+3y≤15 dan 2x+5y≥10 menjadi persamaan:
5x+3y=15
2x+5y=10
Persamaan 5x+3y=15
Saat x=0 maka
5(0)+3y=15
3y=15
y=5
Titik potongnya: (0,5)
Saat y=0 maka
5x+3(0)=15
5x=15
x=3
Titik potongnya: (3,0)
Persamaan 2x+5y=10
Saat x=0 maka
2(0)+5y=10
5y=10
y=2
Titik potongnya: (0,2)
Saat y=0 maka
2x+5(0)=10
2x=10
x=5
Titik potongnya: (5,0)
Langkah 2
Buat grafik dari titik-titik yang dihasilkan persamaan 5x+3y=15 dan 2x+5y=10
Langkah 3
Ambil titik uji
Misalkan: (0,0)
Pertidaksamaan: 5x+3y≤15
5(0)+3(0)≤15
0≤15 [benar]
Pertidaksamaan: 2x+5y≥10
2(0)+5(0)≥10
0≥0 [salah]
Langkah 4
Grafik daerah penyelesaian
Untuk pertidaksamaan 5x+3y≤15 daerah penyelesaiannya berada di sebelah kiri garis karena 0≤15[benar] sedangkan untuk pertidaksamaan 2x+5y≥10 daerah penyelesaiannya berada di kanan garis karena 0≥10 [salah].
Berikan arsir yang berbeda untuk kedua pertidaksamaan agar kita dapat melihat daerah penyelesaiaanya. Perhatikan gambar berikut:
Dengan demikian, daerah penyelesaian pada bidang koordinat cartesiusnya adalah sebagai berikut:
Contoh 3
Tentukan daerah penyelesaian sistem pertidaksamaan linear berikut pada bidang koordinat cartesius!
3x-2y≤12
2x+y≤6
x≥0
y≥0
Jawaban:
Langkah 1
Ubah pertidaksamaan 3x-2y≤12 dan 2x+y≤6 menjadi persamaan:
3x-2y=12
2x+y=6
Persamaan 3x-2y=12
Saat x=0 maka
3(0)-2y=12
-2y=12
y=-6
Titik potongnya: (0,-6)
Saat y=0 maka
3x-2(0)=12
3x=12
x=4
Titik potongnya: (4,0)
Persamaan 2x+y=6
Saat x=0 maka
2(0)+y=6
y=6
Titik potongnya: (0,6)
Saat y=0 maka
2x+0=6
2x=6
x=3
Titik potongnya: (3,0)
Langkah 2
Buat grafik dari titik-titik yang dihasilkan persamaan 3x-2y=12 dan 2x+y=6
Langkah 3
Ambil titik uji
Misalkan: (0,0)
Pertidaksamaan: 3x-2y≤12
3(0)-2(0)≤12
0≤12 [benar]
Pertidaksamaan: 2x+y≤6
2(0)+0≤6
0≤6 [benar]
Langkah 4
Grafik daerah penyelesaian
Untuk pertidaksamaan 3x-2y≤12 daerah penyelesaiannya berada di sebelah kiri garis karena 0≤12[benar] demikian pula untuk pertidaksamaan 2x+y≤6 daerah penyelesaiannya berada di kiri garis karena 0≤6 [benar].
Berikan arsir yang berbeda untuk kedua pertidaksamaan agar kita dapat melihat daerah penyelesaiaanya. Perlu kita perhatikan juga bahwa pada soal diberikan x≥0 dan y≥0. Perhatikan gambar berikut:
Dengan demikian, daerah penyelesaian pada bidang koordinat cartesiusnya adalah sebagai berikut:
Contoh 4
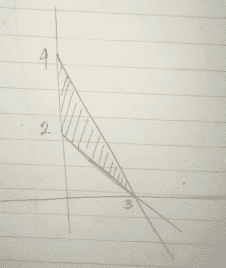
Tentukan sistem pertidaksamaan linear untuk daerah yang diarsir pada bidang koordinat cartesius berikut!
Jawaban:
Langkah 1 [Garis 1]
Mencari Persamaan Garis 1
Garis 1 melalui titik (3,0) dan (0,2) sehingga persamaan garisnya yaitu:
ax+by=ab
Diketahui: a=2 dan b=3 maka:
2x+3y=6
Karena daerah penyelesaian berada di kanan titik (3,0) dan (0,2) dan garisnya tidak putus-putus maka pertidaksamaannya yaitu 2x+3y≥6
Langkah 2 [Garis 2]
Mencari Persamaan Garis 2
Garis 1 melalui titik (3,0) dan (0,4) sehingga persamaan garisnya yaitu:
ax+by=ab
Diketahui: a=4 dan b=3 maka:
4x+3y=12
Karena daerah penyelesaian berada di kiri titik (3,0) dan (0,2) dan garisnya tidak putus-putus maka pertidaksamaannya yaitu 4x+3y≤12
Langkah 4
Daerah penyelesaiannya berada di KUADRAN 1 maka daerah penyelesaian pertidaksamaannya yaitu x≥0 dan y≥0
Langkah 5
Dengan demikian sistem pertidaksamaan linear untuk daerah yang di arsir pada grafik diatas yaitu:
2x+3y≥6
4x+3y≤12
x≥0
y≥0
Contoh 5
Tentukan sistem pertidaksamaan linear untuk daerah yang diarsir pada bidang koordinat cartesius berikut!
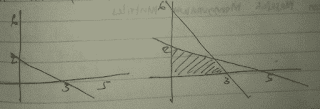
Jawaban:
Langkah 1 [Garis 1]
Mencari Persamaan Garis 1
Garis 1 melalui titik (3,0) dan (0,6) sehingga persamaan garisnya yaitu:
ax+by=ab
Diketahui: a=6 dan b=3 maka:
6x+3y=18
2x+y=6
Karena daerah penyelesaian berada di kiri titik (3,0) dan (0,6) dan garisnya tidak putus-putus maka pertidaksamaannya yaitu 2x+y≤6
Langkah 2 [Garis 2]
Mencari Persamaan Garis 2
Garis 1 melalui titik (5,0) dan (0,2) sehingga persamaan garisnya yaitu:
ax+by=ab
Diketahui: a=2 dan b=5 maka:
2x+5y=10
Karena daerah penyelesaian berada di kiri titik (3,0) dan (0,2) dan garisnya tidak putus-putus maka pertidaksamaannya yaitu 2x+5y≤10
Langkah 4
Daerah penyelesaiannya berada di KUADRAN 1 maka daerah penyelesaian pertidaksamaannya yaitu x≥0 dan y≥0
Langkah 5
Dengan demikian sistem pertidaksamaan linear untuk daerah yang di arsir pada grafik diatas yaitu:
2x+y≤6
2x+5y≤10
x≥0
y≥0
Demikian Contoh Soal dan Jawaban Sistem Pertidaksamaan Linear SMA Kelas 10.
Semoga bermanfaat dan jangan lupa berkunjung kembali.