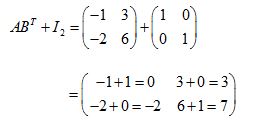Mathematics

sheetmath.com membahas seputar pelajaran matematika

Contoh Soal Matriks dan Operasinya disertai Penyelesaiannya

Pada kesempatan kali ini, akan diberikan 7 nomor untuk soal beserta cara penyelesaiannya tentang matriks dan operasinya.

Nomor 1
Soal: Diberikan mariks A dan B sebagai berikut:

\(A=\begin{pmatrix} 1\\ 2 \end{pmatrix}, B=\begin{pmatrix} -1\\ 3 \end{pmatrix}\)

Tentukan:
\((AB^{T}+I_{2})^{-1}\)
Jawab:
Pertama-tama cari dahulu

\(AB^{T}=\begin{pmatrix} 1\\ 2 \end{pmatrix}\begin{pmatrix} -1 &3 \end{pmatrix}\)
\(=\begin{pmatrix} 1.(-1)=-1 &1.3=3 \\ 2.(-1)=-2 & 3.3=6 \end{pmatrix}\)

Setelah itu tambahkan hasil di atas dengan \(I_{2}\) sehingga akan seperti berikut:

 

 

 

 

Kemudian hasil di atas, di inverskan. Pertama-tama cari dahulu nilai determinan dari matriks yang sudah diperoleh yaitu sebagai berikut:

\(AB^{T}+I_{2}=0.7-3(-2)=6\)

Dengan demikian:

\((AB^{T}+I_{2})^{-1}=\frac{1}{6}\begin{pmatrix} 7 &-3 \\ 2 &0 \end{pmatrix}=\begin{pmatrix} 7/6 &-1/2 \\ 1/3& 0 \end{pmatrix}\)

Baca juga:

2. Transpos Matriks Dan Determinan Suatu Matriks Segi

Nomor 2
Soal: Diberikan matrik A berukuran 2×2 dan matriks B berukuran 3×2 sebagai berikut:

\(A=\begin{pmatrix} 3 &-1 \\ 1 &-2 \end{pmatrix}, B=\begin{pmatrix} 1 &-1 \\ 2 &0 \\ 6 &1 \end{pmatrix}\)

Tentukan:
a] \(AB^{T}\)
b] Pangkat matriks B, dan berikan alasannya.
Jawab:
a] Petama-tama, ubah dahulu matriks B menjadi matrik B yang di transpos sebagai berikut:

\(B=\begin{pmatrix} 1 &-1 \\ 2 & 0\\ 6 &1 \end{pmatrix}\rightarrow B^{T}=\begin{pmatrix} 1 &2 &6 \\ -1 &0 &1 \end{pmatrix}\)

Setelah itu, tentukan \(AB^{T}\) sebagai berikut:
\(AB^{T}=\begin{pmatrix} 3 &-1 \\ 1 & -2 \end{pmatrix}\begin{pmatrix} 1 &2 &6 \\ -1 &0 &1 \end{pmatrix}\)
         \(=\begin{pmatrix} 3(1)+(-1)(-1)=4 &3(2)+(-1)(0)=6 &3(6)+(-1)(1)=17 \\ 1(1)+(-2)(-1)=3 &1(2)+(-2)(0)=2 &1(6)+(-2)(1)=4 \end{pmatrix}\)
b] Untuk menjawab pertanyaan b, ada 2 cara penyelesaian yaitu sebagai berikut:

Cara 1: Ambil anak matriks dari matriks B berukuran 2×2 sebagai berikut:

\(\hat{B}=\begin{pmatrix} 1 &-1 \\ 2 &0 \end{pmatrix}\)

karena :
 \(\left | \hat{B} \right |=2\neq 0\)
maka p(B) = 2

Cara 2: Lakukan serangkaian Operasi Baris Dasar (OBD) terhadap matriks B sehingga menjadi matriks mirip sgitiga atas. Seperti berikut ini:
\(B=\begin{pmatrix} 1 &-1 \\ 2 &0 \\ 6 &1 \end{pmatrix}\)

 

 

 

 

 

 

 

Terlihat bahwa p(B) = 2

Nomor 3
Soal: Diberikan matriks B sebagai berikut:

\(B=\begin{pmatrix} 0 &1 &0 \\ -1 &1 &1 \\ 1 &0 &0 \end{pmatrix}\)

Tentukan: \(B^{-1}\) dengan metode matriks adjoin.
Jawab:
Pertama-tama, tentukan dahulu matriks kofaktornya sebagai berikut:
Matriks kofaktor \(C=(a_{ij})\) dengan:

 

 

 

 

 

 

 

 

 

Sehingga matriks kofaktornya sebagai berikut:

\(C=\begin{pmatrix} 0 &1 &-1 \\ 0 &0 &1 \\ 1 &0 &1 \end{pmatrix}\)

Dengan mengambil baris ke-3 dari matriks B, diperoleh:

\(\left | B \right |=\alpha _{31}\alpha _{31}+\alpha _{32}\alpha _{32}+\alpha _{33}\alpha _{33}=1.1+0.0+0.0=1\)

Maka:

\(B^{-1}=\frac{1}{\left | B \right |}C^{T}=\frac{1}{1}\begin{pmatrix} 0 &1 &-1 \\ 0 &0 &1 \\ 1 &0 &1 \end{pmatrix}^{T}\)
\(=\begin{pmatrix} 0 &0 &1 \\ 1 &0 &0 \\ -1 &1 &1 \end{pmatrix}\)

Nomor 4
Soal: Diberikan matriks-matriks A dan B sebagai berikut:
\(A=\begin{pmatrix} 1 &-1 &2 \\ 0 &3 &4 \end{pmatrix}, B=\begin{pmatrix} 4 &0 &-3 \\ -1 &-2 &3 \end{pmatrix}\)

Jika ada, tentukan:
a] \(AB^{T}\)
b] \((AB^{T})^{-1}\)
Jawab:
a] Akan diperoleh seperti dibawah ini:

\(AB^{T}=\begin{pmatrix} 1 &-1 &2 \\ 0 &3 &4 \end{pmatrix}\begin{pmatrix} 4 &-1 \\ 0 &-2 \\ -3 &3 \end{pmatrix}\)
\(=\begin{pmatrix} -2 &7 \\ -12 &6 \end{pmatrix}\)

b] Untuk mencari matriks invers dari jawaban (a) maka terlebih dahulu tentukan nilai determinannya, yaitu: (-2)(6) – (-12)(7) = 72. Sehingga,

\((AB^{T})^{-1}=\frac{1}{72}\begin{pmatrix} 6 &-7 \\ 12 &-2 \end{pmatrix}=\begin{pmatrix} 1/12 &-7/72 \\ 1/6 & -1/36 \end{pmatrix}\)

Nomor 5
Soal: Diberikan matriks A dan B sebagai berikut:

\(A=\begin{pmatrix} 1 &-1 \\ 3 &2 \end{pmatrix}, B=\begin{pmatrix} 3 &-4 \end{pmatrix}\)

Tentukan:
a] 3BA – 2B
b] \(\det(5A^{T})\)
Jawab:
a] Akan diperoleh sebagai berikut:
\(3BA-2B=3\begin{pmatrix} 3 &-4 \end{pmatrix}\begin{pmatrix} 1 &-1 \\ 3 &2 \end{pmatrix}-2\begin{pmatrix} 3 &-4 \end{pmatrix}\)
\(3BA-2B=\begin{pmatrix} 27 &-33 \end{pmatrix}-\begin{pmatrix} 6 &-8 \end{pmatrix}=\begin{pmatrix} -33 &-25 \end{pmatrix}\)
b] Pertama-tama cari dahulu

\(5A^{T}=5\begin{pmatrix} 1 &-1 \\ 3 &2 \end{pmatrix}^{T}= 5\begin{pmatrix} 1 &3 \\ -1 &2 \end{pmatrix}\)
\(=\begin{pmatrix} 5 &15 \\ -5 &10 \end{pmatrix}\)

Kemudian determinankan hasil matriks tersebut sebagai berikut:

\(\det(5A^{T})=5(10)-(-5)(15)=125\)

Nomor 6
Soal: Diketahui matriks-matriks A dan B sebagai berikut:

\(A=\begin{pmatrix} 2 &1 &-2 \\ 0 &1 &0 \\ 0 &2 &0 \end{pmatrix}, B=\begin{pmatrix} 1 &2 &3 \end{pmatrix}\)

Tentukan:
a] \(AB^{T}\)
b] pangkat matriks A
Jawab:
a] Akan diperoleh:

 

 

 

 

 

b] Karena baris ke tiga merupakan kelipatan baris ke dua maka |A| = 0 sehingga p(A) < 3. Dengan mengambil salah satu anak matriks berukuran 2 x 2 maka akan di peroleh sebagai berikut:

\(\begin{vmatrix} 2 &1 \\ 0 &1 \end{vmatrix}=2\neq 0\)

Sehingga p(A) = 2.
Atau dengan cara lain, yaitu melakukan Operasi Baris Dasar (OBD) sehingga A menjadi matriks segitiga atas seperti di bawah ini:

\(\begin{pmatrix} 2 &1 &-2 \\ 0 &1 &0 \\ 0 &2 &0 \end{pmatrix}\)
\(E_{32(-2)}\begin{pmatrix} 2 &1 &-2 \\ 0 &1 &0 \\ 0 &2+1(-2)=0 &0 \end{pmatrix}\)

Diperoleh, p(A) = 2

Baca Juga :

2. Operasi Baris Dasar Terhadap Matriks

Nomor 7
Soal: Diberikan matriks A dan C sebagai berikut:

\(A=\begin{pmatrix} 1 & 2\\ 0&1 \end{pmatrix},C=\begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &2 \end{pmatrix}\)

Tentukan: matriks X yang memenuhi

\(AXC=\begin{pmatrix} 1 & 2\\ 0&1 \end{pmatrix},C=\begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \ \end{pmatrix}\)

Jawab:

 

 

 

 

 

Sampai disini yaaa Gengs.

 
Artikel sebelumnya Contoh Soal Terapan Matriks pada Sistem Persamaan Linear
Artikel selanjutnya Soal dan Jawaban Limit dan Kekontinuan

akulingiyai

Artikel Terbaru

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Kembali ke atas