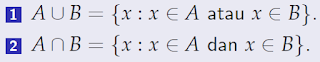Sistem Bilangan Real
Â
Â
Â
Ilustrasinya
Â
Â
Â
Garis Real
1. R diasosiasikan sebagai garis lurus
  x anggota dari R diasosiasikan sebagai suatu titik di garis
 Â
Â
Â
Â
Â
2. Titik acuan: bilangan 0
   Bilangan real positif x terletak x unit di kanan 0Â
   Bilangan real positif -x terletak x unit di kiri 0Â
Â
Urutan
Definisi (Relasi Urutan)
1. Relasi urutan < (dibaca lebih kecil daripada) didefinisikan olehÂ
  x < y jika dan hanya jika y – x positif.Â
2. Relasi urutan <= (dibaca lebih kecil daripada atau sama dengan)
didefinisikan olehÂ
didefinisikan olehÂ
  x <= y jika dan hanya jika y – x positif atau nol
Â
Sifat-Sifat Urutan
1. Trikotomi
  Jika x dan y adalah bilangan-bilangan, maka tepat satu di antara
yang berikut berlaku:
yang berikut berlaku:
  x < y atau x = y atau x > y
2. Ketransitifan
  Jika x < y dan y < z, maka x < z Â
3. Penambahan
  x < y jika dan hanya jika x + z < y + z
4. Perkalian
  Ketika z positif, x < y jika dan hanya jika xz < yz
   Ketika z negatif, x < y jika dan hanya jika xz > yzÂ
   Ketika z negatif, x < y jika dan hanya jika xz > yzÂ
Â
IntervalÂ
Definisi (Interval)
Interval adalah himpunan bilangan real yang didefinisikan dan
dilambangkan sebagai berikut
dilambangkan sebagai berikut
Â
Â
Gabungan dan Irisan
Definisi
Misalkan A dan B merupakan interval
Â
Pertidaksamaan
Definisi (Pertidaksamaan)
Pertidaksamaan adalah pernyataan matematik yang memuat salah satu relasi urutan <, >, <= , atau >= .
Definisi (Penyelesaian Pertidaksamaan)
Penyelesaian pertidaksamaan adalah semua bilangan real yang memenuhi pertidaksamaan tersebut
Â
Menyelesaikan pertidaksamaan:
- Dengan sifat urutan
- Dengan garis bilangan bertandaÂ
Nilai MutlakÂ
Definisi (Nilai Mutlak)
Nilai mutlak suatu bilangan real x, dinyatakan oleh |x|, didefinisikan
sebagaiÂ
sebagaiÂ
Â
Â
 yang perlu di perhatikan:
Sifat-Sifat Nilai Mutlak
1. Misalkan a, b anggota R dan n anggota Z, maka
Â
Â
2. Misalkan x, y anggota R dan a > 0, maka
Â
3. Misalkan x, y anggota R dan n anggota Z, maka
Â
Â
Demikian pembahasan tentang “Interval, Pertidaksamaan, dan Nilai Mutlak“. Semoga bermanfaat.
