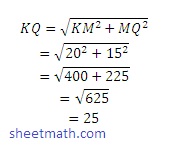Teorema Pythagoras Kelas 8 – Contoh Soal Dan Pembahasan

Pada suatu segitiga, berlaku teorema Pythagoras sebagai berikut:
Diketahui a,b, dan c adalah panjang sisi-sisi sebuah segitiga. Misalkan sisi miring adalah c dan panjang sisi lainnya adalah a dan b, maka:
1. Jika c²=a²+b², segitiga tersebut adalah siku-siku

2. Jika c²<a²+b², segitiga tersebut adalah lancip

3. Jika c²>a²+b², segitiga tersebut adalah tumpul

Teorema Pythagoras sering diaplikasikan untuk menghitung:
1. Jarak dua titik pada bidang koordinat,
2. Panjang diagonal persegi dan persegi panjang,
3. Panjang diagonal sisi dan diagonal ruang pada kubus dan balok,
4. Keliling dan luas bangun datar menggunakan teorema pythagoras.

Tanpa basa basi, kita langsung saja latihan soal-soal yang sudah saya sediakan.SOAL PERTAMA
Diketahui segitiga OQR memiliki panjang PQ=13 cm QR=5 cmdan PR=12 cm.
Tunjukkan bahwa :
1. Segitiga PQR siku-siku
2. Sudut manakah yang merupakan sudut siku-siku?

PEMBAHASAN:
Untuk menjawab soal bagian (1) ini yang perlu kita ketahui yaitu bahwa suatu segitiga adalah siku siku apabila c² =a²+b² dimana c adalah sisi miring pada segitiga.

Pada soal diatas tidak dikatakan sisi mana yang merupakan sisi miring pada segitiga PQR, namun biasanya pada segitiga sisi yang mempunyai sisi terpanjang itulah yang merupakan sisi miringnya.Pada soal ini sisi terpanjang yaitu PQ=13 cm. sehingga kuadrat dari sisi terpanjang yaitu 13² = 169.

Sedangkan kuadrat dari kedua sisi QR dan PR adalah 5² =25 dan 12² = 144 sehingga jumlah kedua kuadrat sisi adalah 25+144 = 169.

Setelah menghitung jumlah kedua sisi, diperoleh hubunga berikut c² =a²+b² yang berarti berlaku teorema Pythagoras. Dengan demikian segitiga PQR siku-siku.

SOAL KEDUA
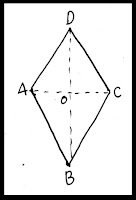
Diketahui belah ketupat ABCD dengan titik O merupakan titik potong kedua diagonalnya. Jika panjang AC=10√3cm dan besar segitiga DAO=30°, berapakah keliling belah ketupat tersebut?

PEMBAHASAN:
Pertama-tama kita gambarkan terlebih dahulu belah ketupat ABCD seperti berikut ini.

Agar kita dapat menghitung keliling belah ketupat, kita harus mengetahui panjang sisinya. Karena rumus yang akan kita gunakan yaitu 4xsisi.Dari gambar diatas, dapat kita lihat bahwa titik O membagi diagonal AC menjadi dua sama panjang sehingga:
AO=OC=5√3

Segitiga AOD siku-siku di O yang salah satu sudutnya 30° sehingga berlaku AO:OD:AD=5√3:1:2

Selanjutnya kita akan menghitung panjang AD.

Dalam belah ketupat, sisi-sisinya sama panjang sehingga:
Keliling= 4xAD=4×10=40. Dengan demikian kelulung belah ketupat ABCD adalah 40 cm

SOAL KETIGA
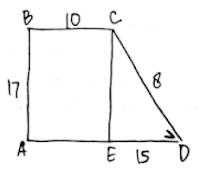
Perhatikan gambar bangun datar berikut ini:

Hitunglah keliling dan luas dari bangun datar tersebut.PEMBAHASAN
Untuk menghitung keliling bangun datar tersebut kita harus mengetahui panjang semua sisi-sisinya. Sedangkan apabila kita perhatikan baik-baik pada gambar tersebut , semua sisinya telah diketahui kecuali sisi CE dan AB (CE=AB).
Untuk mencari sisi CE kita perhatikan segituga CDE dengan siku-siku di D.Perhitungannya akan seperti berikut ini.

Dengan demikian, keliling = AB+BC+CD+DE+AE=17+10+8+15+10=60 cm
Selanjutnya, kita akan menghitung luas bangun datar. Pada bangun datar tersebut terdapat bangun segitiga dan persegi panjang. Kita akan menjumlahkan luas segitiga dan luas persegi panjang. Seperti berikut ini.
LUAS=LUAS  CDE + LUAS ABCD
=(1/2 x CD x DE)   +   (AB x BC)
=(1/2 x 8 x 15)   +   (17 x 10)
= 60 + 170 = 230
Sehingga, luas bangun datar tersebut yaitu 230 cm²

SOAL KEEMPAT
Perhatikan sebuah gambar balok berikut ini. Diketahui alas balok KLMN berbentuk persegi panjang dengan panjang KL=16cm dan LM= 12cm, sudut KLM =90°, panjang KM=20cm dan MQ=15cm

Tentukan:
a. Panjang diagonal sisi KM
b. Panjang diagonal ruang KQPEMBAHASAN
a. Panjang KM
Alas balok KLMN berbentuk persegi panjang dengan panjang KL=16cm dan LM= 12cm. karena  sudut KLM =90° maka panjang KM ditentukan menggunakan teorema Pythagoras.

Maka, panjang diagonal sisi KM adalah 20 cm.

b. Panjang KQ
Perhatikan segitiga KMQ siku-siku di M dengan panjang KM=20cm dan MQ=15cm. garis KQ merupakan diagonal ruang. Panjang KQ ditentukan menggunakan teorema Pythagoras.

Maka, panjang diagonal ruang KQ adalah 25 cm.

SOAL KELIMA
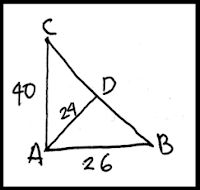
Perhatikan segitiga ABC dibawah ini.

Garis AD merupakan garis tinggi segitiga yang ditarik dari titik sudut A. panjang  AB =26cm, AC=40cm dan AD=24cm. Tentukan:
a. Panjang BC
b. Luas segitiga ABCPEMBAHASAN
a. Panjang BC merupakan gabungan antara panjang BD dan DC
Menentukan panjang BD
Perhatikan segitiga ABD siku-siku di D.
AB² =BD² + AD²

26² = BD² + 24²

676 = BD² +576

BD² = 676-576

BD² = 100

BD=10
JADI, panjang BD adalah 10 cmMenentukan panjang DC
PERHATIKAN segitiga ADC siku-siku di D
AC² =AD² + DC²

40² = 24² + DC²

1600 = 576 +DC²
DC² = 1600-576

DC² = 1024

DC=32
JADI, panjang DC adalah 32 cm
Dengan demikian panjang BC = BD+DC=10+32=42cmb. Menentukan luas segitiga
Luas =½  x alas x tinggi = ½ x BC x AD = ½ x 42 x 24 = 504 cm²

SOAL KEENAM
Perhatikan segitiga siku-siku sama kaki berikut ini.

Tentukan perbandingan panjang sisi-sisi segitiga siku-siku sama kaki.PEMBAHASAN
Panjang AB=BC=CA
Sudut BAC=sudut BCA=sudut CAB
AC² = AB² + BC²

AC²=a² + a²

AC²=2a²

AC=a√2

Perbandingan panjang sisi-sisi  segitiga ABC yaitu:
AB:BC:AC =a:a:a√2= 1:1:√2

Nahhhh bagaimana?? Mudah bukan.
Sampai disini dulu ya Gengs latihan soalnya. Jangan lupa kunjungi artikel yang lainnya.

Semoga bermanfaat.