Soal Matematika Kelas 9 – Pada contoh soal matematika kelas 9 kali ini, saya akan memberikan contoh-contoh soal dari: 1) Bilangan berpangkat dan bentuk akar, 2) Persamaan kuadrat, 3) Fungsi kuadrat, 4) Transformasi geometri, 5) Kekongruenan dan kesebangunan 6) Bangun ruang sisi lengkung. Bukan hanya contoh soalnya saja, saya pun memberikan jawabannya. Sehingga, Gengs bisa jadikan panduan untuk belajar di rumah.
Soal 1
Tentukan hasil operasi berikut menjadi bentuk pangkat bulat positif.
a. 3⁴ × 3⁷
b. 5⁸ : 5²
Jawaban:
a. 3⁴ × 3⁷ = 3⁴⁺⁷ = 3¹¹
b. 5⁸ : 5² = 5⁸⁻² = 5⁶
Soal 2
Tentukan nilai n pada persamaan berikut.
a. (\(2^n\)) = 32
b. (\((½)^{n-1}\)) = 4
Jawaban:
a. (\(2^n\)) = 32
(\(2^n\)) = 2⁵
n = 5
Jadi, nilai n pada persamaan (\(2^n\)) = 32 adalah 5.
b. (\((½)^{n-1}\)) = 4
(\((2⁻¹)^{n-1}\)) = 4
(\(2^{-1× (n-1)}\)) = 2²
(\(2^{-n+1}\)) = 2²
-n + 1 = 2
-n = 1
n = -1
Jadi, nilai n pada persamaan (\((½)^{n-1}\)) = 4 adalah -1.
Soal 3
Tentukan hasil operasi bilangan berpangkat rasional berikut.
a. (\(4^½\)) – \(16^¾\) + \(32^⅕\)
b. \(5^¾\) × \(25^¼\) × \(125^⁻⅔\)
Jawaban:
a. \(4^½\) – \(16^¾\) + \(32^⅕\)
= \((2²)^½\) – \((2⁴)^¾\) + \((2⁵)^⅕\)
= \(2^{2×½}\) – \(2^{4×¾}\) + \(2^{5×⅕}\)
= 2¹ – 2³ + 2¹
= 2 – 8 + 2
= -4
b. \(5^¾\) × \(25^¼\) × \(125^⁻⅔\)
= \(5^¾\) × \((5²)^¼\) × \((5³)^⁻⅔\)
= \(5^¾\) × \(5^{2×¼}\) × \(5^{3×(-⅔)}\)
= \(5^¾\) × \(5^½\) × 5⁻²
= \(5^{¾+½+(-2)}\)
= \(5^{-¾}\)
Pelajari Juga : 30 Soal Bilangan Berpangkat dan Bentuk Akar Plus Jawaban Kelas 9
Soal 4
Tentukan hasil operasi dari 2√12 + 9√3 – 3√27
Jawaban:
2√12 + 9√3 – 3√27
= 2√(4 × 3) + 9√3 – 3√(9 × 3)
= 2 × √4 × √3 + 9√3 – 3 × √9 × √3
= 2 × 2 × √3 + 9√3 – 3 × 3 × √3
= 4√3 + 9√3 – 9√3
= (4 + 9 – 9) √3
= 4√3
Soal 5
Tentukan nilai p jika diketahui:
a. Persamaan x² + 6x – p = 0 dengan akar x₁ = -9 dan x₂ = 3.
b. Persamaan (p + 1) x² – x + 8 = 0 dengan diskriminan -95
Jawaban:
a. Diketahui persamaan x² + 6x – p = 0 dengan akar x₁ = -9 dan x₂ = 3
Substitusikan salah satu akar persamaan kuadrat, misalnya x₁=-9, ke dalam persamaan x² + 6x – p = 0.
x² + 6x – p = 0
(-9)² + 6(-9) – p = 0
81 + (-54) – p = 0
27 – p = 0
p = 27
Jadi, nilai p adalah 27.
b. Dari persamaan kuadrat (p + 1)x² – x + 8 = 0 diperoleh a = p + 1, b = -1 dan c = 8.
D = b² – 4ac
-95 = (-1)² – 4(p + 1)(8)
-95 = 1 – 4(8p + 8)
-95 = 1 – 32p – 32
-95 = -32p – 31
32p = -31 + 95
32p = 64
p=2
Jadi, nilai p adalah 2.
Soal 6
Persamaan kuadrat (m – 2)x² + mx +(m/4) + 1 = 0 mempunyai dua akar real berbeda. Tentukan nilai m yang memenuhi.
Jawaban:
Dari persamaan (m – 2)x² + mx + (m/4) + 1 = 0 diperoleh a = m – 2, b = m dan c = (m/4) + 1.
Persamaan kuadrat mempunyai dua akar real berbeda jika D>0.
D > 0
b² – 4ac > 0
m² – 4(m – 2)( (m/4) + 1) > 0
m² – (4m – 8) ((m/4) + 1) > 0
m² – (m² + 4m – 2m – 8) > 0
-2m + 8 > 0
2m < 8
m < 4
Jadi, nilai m yang memenuhi adalah m < 4.
Soal 7
Tentukan akar-akar dari persamaan kuadrat x² + 14x + 48 = 0
Jawaban:
Dari persamaan kuadrat x² + 14x + 48 = 0 diperoleh a = 1, b = 14 dan c = 48.
Akan dipilih p dan q yang memenuhi syarat :
p + q = b = 14
pq = c = 48
Dipilih p = 8 dan q = 6
x² + 14x + 48 = 0
(x + 8)(x + 6) = 0
x + 8 = 0 atau x + 6 = 0
x = -8 atau x = -6
Jadi, akar-akarnya adalah x₁ = -8 atau x₂ = -6.
Soal 8
Diketahui persamaan kuadrat 3x² – x + 6 = 0 dengan akar-akar α dan β. Tentukan:
a. Persamaan kuadrat yang mempunyai akar-akar 3α dan 3β
b. persamaan kuadrat yang mempunyai akar-akar α+β dan αβ
Jawaban:
a. Dari persamaan kuadrat 3x² – x + 6 = 0 diperoleh a = 3, b = -1 dan c = 6.
α dan β adalah akar-akar persamaan kuadrat tersebut sehingga diperoleh:
α + β = -(b/a) = -(-1/3) = ⅓
αβ = c/a = 6/3 = 2
Persamaan kuadrat yang dicari mempunyai akar-akar 3α dan 3β sehingga:
3α + 3β = 3(α + β) = 3 × ⅓ = 1
3α × 3β = 9αβ = 9 × 2 = 18
Persamaan kuadrat akar-akarnya 3α dan 3β sehingga:
x² – (3α + 3β)x + 3α × 3β = 0
x² – x + 18=0
Jadi, persamaan kuadrat yang dicari adalah x² – x + 18 = 0.
b. Persamaan kuadrat yang dicari mempunyai akar-akar α+β dan αβ sehingga:
(α + β) + αβ = ⅓ + 2 = 7/3
(α + β) × αβ = ⅓ × 2 = ⅔
Persamaan kuadrat akar-akarnya α+β dan αβ sehingga:
x² -((α + β) + αβ) x + (α + β) × αβ = 0
x² – (7/3)x + ⅔=0
3x² – 7x + 2 = 0
Jadi, persamaan kuadrat yang dicari adalah 3x² – 7x + 2 = 0.
Soal 9
Jika grafik fungsi kuadrat y = f(x) = x² + 8x + 7 digeser ke kanan 5 satuan menghasilkan grafik y = h(x), tentukan titik balik dan titik potong grafik y = h(x) dengan sumbu X dan sumbu Y.
Jawaban:
Menentukan titik balik grafik.
Persamaan grafik fungsi kuadrat y = f(x) = x² + 8x + 7 terlebih dahulu diubah menjadi bentuk y = f(x) = a(x – p)² + q dengan cara seperti berikut.
y = f(x) = x² + 8x + 7
= x² + 8x + (½ × 8)² – (½ × 8)² + 7
= (x² + 8x + 16) – 16 + 7
= (x + 4)² – 9
= (x – (-4))² – 9
Grafik y = f(x) = a(x – p)² + q jika digeser ke kanan 5 satuan akan menghasilkan grafik dengan persamaan y = h(x) = a(x – (p+))² + q.
Diketahui y = f(x) = (x – (-4))² – 9 sehingga diperoleh:
y = h(x) = (x – ((-4) + 5))² – 9
=(x + 4 – 5)² – 9
=(x – 1)² – 9
Grafik fungsi y = f(x) = a(x – p)² + q memiliki titik balik (p,q), maka grafik fungsi y = h(x) = (x – 1)² – 9 memiliki titik balik (1 , -9)
Menentukan titik potong grafik y = h(x) dengan sumbu X.
Grafik memotong sumbu X jika y = h(x) = 0
(x – 1)² – 9 = 0
(x – 1)² – 3² = 0
((x – 1) + 3)((x – 1) – 3) = 0
(x + 2)(x – 4) = 0
x +2 = 0 atau x – 4 = 0
x =-2 atau x = 4
Dengan demikian, grafik y = h(x) memotong sumbu X di titik (-2,0) dan (4,0).
Menentukan titik potong grafik y = h(x) dengan sumbu Y.
Grafik memotong sumbu Y jika x = 0
Nilai fungsi y = h(x) di x = 0 adalah y = h(0)
y = h(0) = (0 – 1)² – 9 = 1 – 9 = -8
Dengan demikian, grafik memotong sumbu Y di titik (0,-8)
Jadi, grafik fungsi y = h(x) memotong sumbu X di titik (-2,0) dan (4,0) serta memotong sumbu Y di titik (0,-8).
Soal 10
Diketahui persamaan grafik fungsi kuadrat f(x) = ax² + bx + c dengan a # 0. Gambarkan sketsa grafik y = f(X) yang memiliki sifat a > 0, b > 0, c < 0 dan D > 0.
Jawaban:
Nilai a > 0 sehingga grafik terbuka ke atas.
Absis titik balik adalah xₚ = -(b/2a).
Nilai a>0 dan b>0 sehingga (b/2a) > 0 dan xₚ = -(b/2a) < 0. Nilai xₚ<0 sehingga titik balik grafik di kiri sumbu Y. Nilai c<0 sehingga grafik memotong sumbu Y negatif. Nilai D>0 sehingga grafik memotong sumbu X.
Sketsa grafik fungsi kuadrat y=f(x) yang sesuai dengan sifat sifat tersebut sebagai berikut:

Soal 11
Tentukan persamaan grafik fungsi kuadrat yang memiliki titik puncak (-2 , 16) dan melalui titik (1 , 7).
Jawaban:
Langkah-langkah menentukan persamaan grafik fungsi kuadrat y = f(x) sebagai berikut.
Langkah 1: Menentukan persamaan y = f(x) secara umum.
Grafik memiliki titik puncak (-2 , 16) sehingga persamaan grafik secara umum:
y = f(x) = a(x – (\(x_A\)))² + (\(y_A\))
= a(x – (-2))² + 16
= a(x +2)² + 16
Langkah 2: Menentukan nilai a
Grafik melalui titik B(1,7), sehingga diperoleh:
(\(y_B\)) = f(\(x_B\))
(\(y_B\)) = a(\(x_b\) + 2)² + 16
7 = a(1 + 2)² + 16
-9 = 9a
a = -1
Langkah 3: Mensubstitusikan nilai a ke dalam persamaan y = f(x) secara umum.
Substitusikan nilai a = -1 ke dalam persamaan grafik fungsi kuadrat y = f(x) = a(x + 2)² + 16 sehingga diperoleh:
Y = f(x) = a(x + 2)² + 16
= (-1)(x + 2)² + 16
= (-1)(x² + 4x + 4) + 16
= -x² – 4x – 4 + 16
= -x² – 4x + 12
Jadi, persamaan grafik fungsi kuadrat adalah f(x) = -x² – 4x + 12
Soal 12
Diketahui fungsi kuadrat f(x) = x² – 8x + 4n. jika grafik y=f(x) memotong sumbu X di dua titik, tentukan batas-batas nilai n.
Jawaban:
Grafik fungsi kuadrat f(x) = x² – 8x + 4n memotong sumbu X di dua titik jika memiliki nilai D>0.
Dari persamaan f(x) = x² – 8x + 4n diperoleh nilai a = 1, b = -8 dan c = 4n.
D > 0
b² – 4ac > 0
(-8)² – 4(1)(4n) > 0
64 – 16n > 0
-16n > -64
-n > 4
n < 4
Jadi, batas-batas nilai n adalah n < 4.
Soal 13
Trapesium KLMN mempunyai koordinat titik K(2,4), L(4,3), M(4,2) dan N(2,1). Trapesium KLMN direfleksikan terhadap sumbu X menghasilkan trapesium K’L’M’N’. Gambarlah trapesium KLMN dan K’L’M’N’ pada bidang koordinat kemudian tentukan koordinat titik K’,L’,M’,N’.
Jawaban:
Trapesium KLMN dan trapesium K’L’M’N’ disajikan pada bidang koordinat berikut.
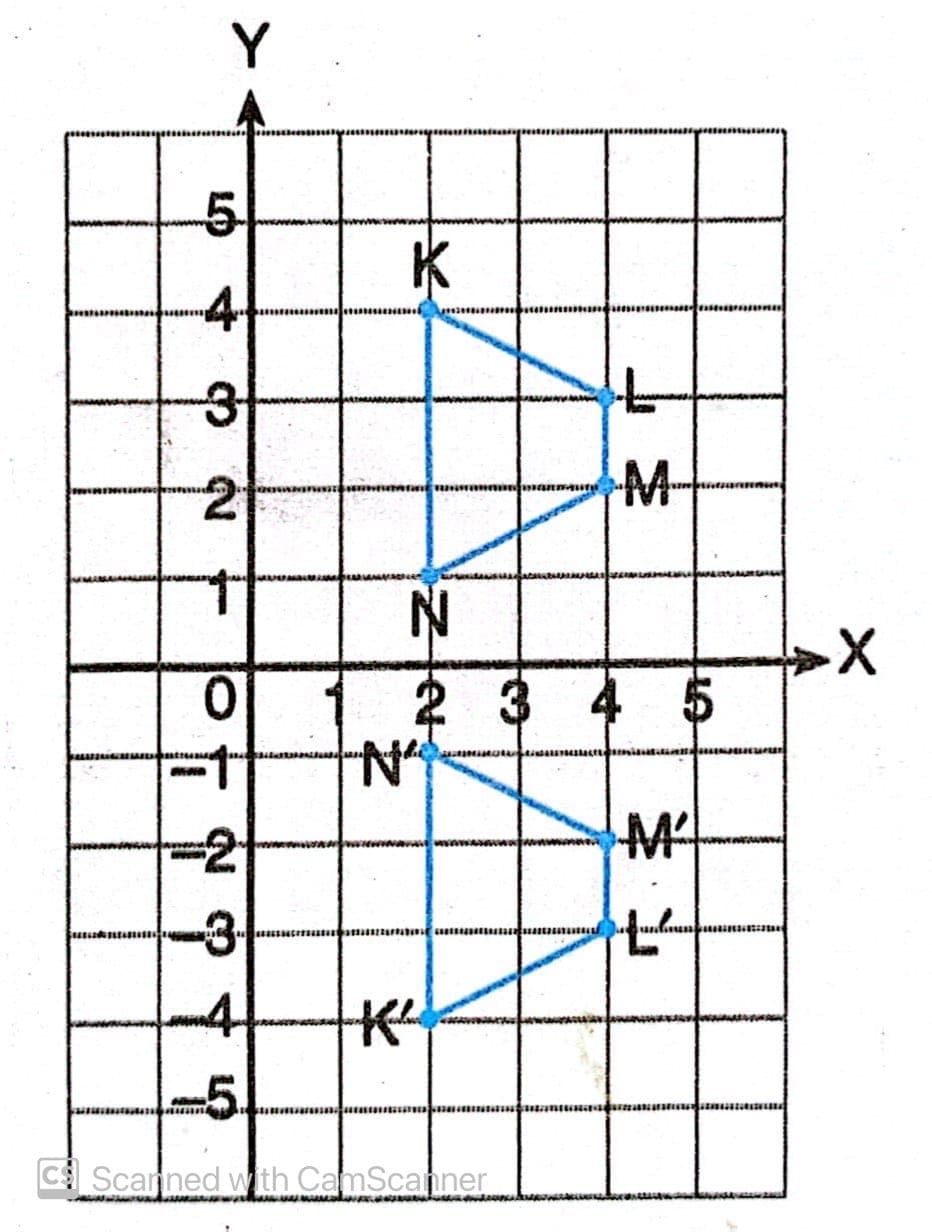
Koordinat titik K’,L’,M’,N’
Dengan menggunakan rumus refleksi terhadap sumbu X diperoleh:
| Koordinat Semula | Hasil Refleksi |
| (x,y) | (x,-y) |
| K(2,4) | K'(2,-4) |
| L(4,3) | L'(4,-3) |
| M(4,2) | M'(4,-2) |
| N(2,1) | N'(2,-1) |
Soal 14
Segitiga PQR mempunyai koordinat titik P(3,1), Q(3,-3) dan R(5,2). Segitiga PQR ditranslasikan oleh T menghasilkan segitiga P’Q’R’ dengan titik P’(-2,4). Tentukan:
a. Translasi T
b. Koordinat titik Q’ dan titik R’
Jawaban:
a. Translasi T
Misalkan translasi T=(a,b)
Hasil translasi titik P(3,1) oleh T=(a,b) adalah P’(3+a,1+b). oleh karena titik P’(-2,4)
Maka:
3 + a = -2
a = -5
1 + b = 4
b = 3
Jadi, translasi T = (-5,3)
b. Koordinat titik Q’ dan titik R’
1) Koordinat titik R’
R’(5-5,2+3)=R’(0,5)
2) Koordinat titik Q’
Q’(3-5,-3+3)=Q’(-2,0)
Jadi, koordinat R’(0,5) dan Q’(-2,0).
Soal 15
Tentukan hasil rotasi setiap titik berikut.
a. Tititk P(3,5) dirotasikan sebesar 90° terhadap titik pusat (0,0)
b. Titik Q(-2,3) dirotasikan sebesar 90° terhadap titik pusat (2,4)
Jawaban:
a. Hasil rotasi titik P
| Koordinat Semula | Hasil Rotasi |
| (x,y) | (-y,x) |
| P(3,5) | P'(-5,3) |
Jadi, hasil rotasi titik P adalah P’(-5,3).
b. Hasil rotasi titik Q
Titik Q(-2,3) maka nilai x=-2 dan y=3.
Hasil rotasi titik (x,y) sebesar 90° terhadap titik pusat (a,b) adalah (x’,y’) dengan:
x’ = b + a – y = 4 + 2 – 3 = 3
y’ = b – a + x = 4 – 2 + (-2) = 0
Jadi, hasil rotasi titik Q adalah Q’(3,0).
Soal 16
Tentukan hasil dilatasi setiap titik berikut.
a. Titik A(3,5) dengan faktor skala -3 terhadap titik pusat (0,0)
b. Titik B(3,-3) dengan faktor skala 3 terhadap titik pusat (4,-4)
Jawaban:
a. Hasil dilatasi titik A
| Koordinat Semula | Hasil Dilatasi |
| (x,y) | (kx,ky) |
| A(3,5) | A’(3(-3),5(-3))=A’(-9,-15) |
Jadi, hasil dilatasi titik A adalah A’(-9,-15)
b. Hasil dilatasi titik B
Titik B(3,-3) maka nilai x=3 dan y=-3.
Titik pusat (4,-4) maka nilai a=4 dan b=-4.
Hasil dilatasi titik (x,y) dengan faktor skala k terhadap titik pusat (a,b) adalah (x’,y’) dengan:
x’ = k(x – a) + a
= 3(3 – 4) + 4
= 3(-1)+4
= 1
y’ = k(y – b) + b
= 3((-3) – (-4)) + (-4)
= 3 – 4
= -1
Jadi hasil dilatasi titik B adalah B’(1,-1)
Soal 17
Sebuah foto ditempelkan pada selembar karton seperti tampak pada gambar di bawah. Disebelah sisi kanan dan kiri foto masih terdapat karton masing-masing selebar 5 cm. apabila foto dan karton sebangun, tentukan luas karton yang tidal tertutup foto.

Jawaban:
Lebar karton = 40 cm
Panjang karton = 50 cm
Lebar foto = 40 -5 – 5 = 30 cm
Foto dan karton sebangun, maka:
\(\frac{Panjang\ foto}{Panjang\ karton}=\frac{Lebar\ foto}{Lebar\ karton}\)
\(\frac{Panjang\ foto}{50}=\frac{30}{40}\)
\(Panjang\ foto=\frac{30\times50}{40}\)
\(Panjang\ foto=37,5\ cm\)
Luas karton = 50 × 40 = 2.000 cm²
Luas foto = 37,5 × 30 = 1.125 cm²
Luas karton yang tidak tertutup foto:
L = Luas karton – Luas foto
= 2.000 – 1.125 = 875 cm²
Jadi, luas karton yang tidak tertutup foto adalah 875 cm².
Soal 18
Perhatikan gambar ΔPQR dan ΔKLM berikut.

a) Tunjukkan bahwa ΔPQR dan ΔKLM kongruen.
b) Sebutkan sudut-sudut yang sama besar dan sisi-sisi yang sama panjang.
Jawaban:
a) Dari gambar diketahui:
1)panjang PR = LM
2) panjang QR = KL
3) m\(\angle\)P = m\(\angle\)M
Oleh karena ΔPQR dan ΔKLM memenuhi syarat s – s – sd, ΔPQR \(\cong\) ΔKLM
b) Sudut-sudut yang sama besar :
1) m\(\angle\)P = m\(\angle\)M (diketahui)
2) m\(\angle\)Q = m\(\angle\)K (didepan sisi PR dan LM)
3) m\(\angle\)R = m\(\angle\)L (sebagai akibat dua sudut lainnya sama besar)
Sisi-sisi yang sama panjang:
1) PR = ML (diketahui)
2) RP = LM (diketahui)
3) PQ = KM (sebagai akibat sisi-sisi yang lain sama panjang)
Soal 19
Perhatikan dua segitiga berikut.

Diketahui m\(\angle\)B = 50° dan m\(\angle\)Q = 40°
a) Buktikan bahwa ΔABC dan ΔPQR sebangun
b)Tuliskan pasangan sudut yang sama besar dan besar sudutnya.
Jawaban:
a) ΔABC siku-siku di B sehingga :
Panjang BC = AB² + AC²=6²+8²=36+64=100=10
ΔPQR siku-siku di R sehingga:
Panjang QR= \(\sqrt{PQ^2+PR^2}=\sqrt{{15}^2+9^2}=\sqrt{225+81}=\sqrt{144}=12\)
Perbandingan sisi-sisi yang bersesuaian:
Sisi terpendek = \(\frac{AB}{PR}=\frac{6}{9}=\frac{2}{3}\)
Sisi sedang = \(\frac{AC}{QR}=\frac{8}{12}=\frac{2}{3}\)
Sisi miring = \(\frac{BC}{PQ}=\frac{10}{15}=\frac{2}{3}\)
Oleh karena perbandingan sisi-sisi yang sesuai sebanding, ΔABC ~ ΔPQR.
Jadi, terbukti bahwa ΔABC dan ΔPQR sebangun.
b) Pasangan sudut yang sama besar :
\(\frac{AB}{PR}\) maka m\(\angle\)C = m\(\angle\)Q = 40°
\(\frac{AC}{QR}\) maka m\(\angle\)B = m\(\angle\)P = 50°
\(\frac{BC}{PQ}\) maka m\(\angle\)A = m\(\angle\)R = 90°
Soal 20
Perhatikan gambar berikut.

a) Tunjukkan bahwa ΔABE ~ ΔCDE
B) Hitung panjang AB
Jawaban:
a) Perhatikan ΔABE dan ΔCDE
m\(\angle\)AEB = m\(\angle\)DEC (bertolak belakang)
m\(\angle\)BAE = m\(\angle\)DCE (dalam bersebrangan)
m\(\angle\)ABE = m\(\angle\)CDE (dalam bersebrangan)
Jadi, ΔABC ~ ΔCDE karena sudut-sudut yang bersesuaian sama besar.
b) Oleh karena ΔABC ~ ΔCDE sisi yang bersesuaian sebanding.
\(\frac{AB}{CD}=\frac{BE}{DE}\)
\(\frac{AB}{10}=\frac{2}{5}\)
5AB=2 ×10
5AB=20
AB=4
Jadi, panjang AB adalah 4 cm.
Soal 21
Sebuah kerucut berada di dalam sebuah tabung seperti gambar di bawah ini.
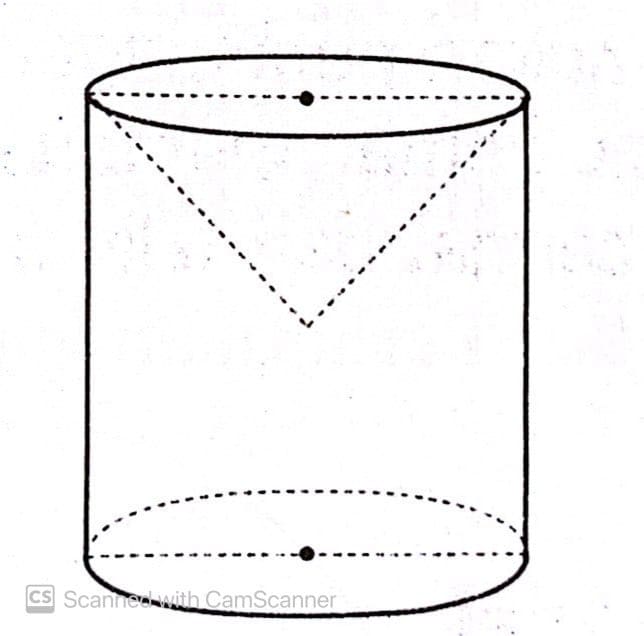
Jika panjang garis pelukis dan tinggi kerucut berturut-turut 26 cm dan 24 cm, tentukan panjang jari-jari tabung.
Jawaban:
Panjang garis pelukis kerucut = s = 26 cm
Tinggi kerucut = t = 24 cm
Jari-jari tabung = jari-jari kerucut = r
r=s²- t²=26²- 24²=676 – 576=100=10
Jadi, panjang jari-jari tabung adalah 10 cm.
Soal 22
Diketahui volume sebuah kerucut 462 cm³ dan tingginya 4 cm. berapa cm panjang diameter kerucut tersebut? (Gunakan π=22/7)
Jawaban:
Diketahui volume kerucut = V = 462 cm³
Tinggi kerucut = t = 4 cm
V = ⅓ × πr² × t
462 = ⅓ × (22/7) × r² × 4
462 = (22/21) × r² × 4
462 × 21 = 88r²
9.702 = 88r²
r² = 9.702/88
r² = 110,25
r = 10,5
Diameter = d = 2r = 2(10,5) = 21
Jadi, panjang diameter kerucut tersebut adalah 21 cm.
Pelajari Juga : Contoh Soal dan Pembahasan Kerucut SMP
Soal 23
Sebuah Perusahaan travel akan membuat balon udara yang berbentuk bola untuk sarana promosi Perusahaan. Jika balon udara yang diinginkan Perusahaan tersebut berjari-jari 3,5 m. Berapa luas bahan yang dibutuhkan untuk membuat sebuah balon udara?
Jawaban:
Bahan yang dibutuhkan = luas permukaan balon
= 4πr²
= 2 × (22/7) ×3,5 × 3,5
= 2 × 22 × 0,5 × 3,5
= 154 m²
Jadi, luas bahan yang dibutuhkan untuk membuat sebuah balon udara adalah 154 m².
Pelajari Juga: Materi Bangun Ruang Sisi Lengkung SMP Kelas 9
Soal 24
Perhatikan gambar berikut.
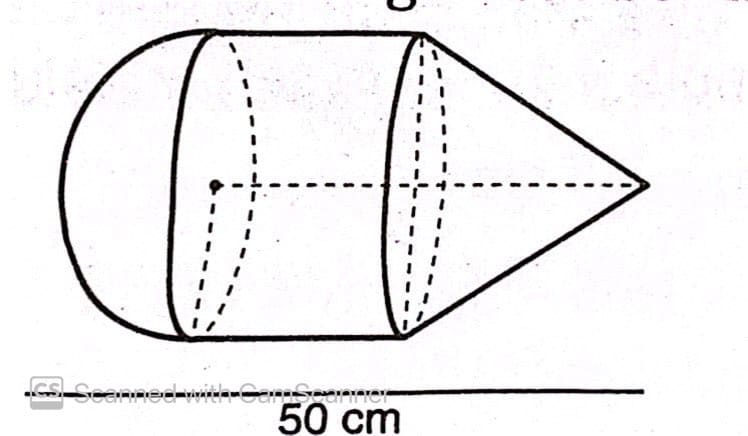
Sebuah benda berbentuk gabungan kerucut, tabung dan belahan bola. Jika panjang diameter bola 20 cm dan tinggi tabung 16 cm, tentukan luas permukaan benda tersebut.
Jawaban:
Diketahui:
Panjang diameter = d = 20 cm
Panjang jari-jari = r = 20/2 = 10 cm
Tinggi tabung = (\(t_T\)) = 16 cm
Tinggi kerucut = (\(t_K\)) = 50 – (10+16) = 24 cm
Panjang garis pelukis kerucut:
\(s=\sqrt{r^2+{t_K}^2}=\sqrt{{10}^2+{24}^2}=\sqrt{100+576}=\sqrt{676}=26\)
Luas permukaan benda:
L = (\(L_{belahan bola}\)) + (\(L_{selimut tabung}\)) + (\(L_{selimut kerucut}\))
= 2πr² + 2πr(\(t_T\)) + πrs
= πr (2r + 2(\(t_T\)) + s)
= 3,14 × 10 (2×10 + 2×16 + 26)
= 3,14 × (20 + 32 + 26)
= 3,14 × 78
= 2.449,2 cm²
Jadi, luas permukaan benda tersebut adalah 2.449,2 cm².
Pelajari Juga : Contoh Soal dan Pembahasan Tabung Kelas 9
Soal 25
Sebuah bak mandi berbentuk tabung dengan diameter 35 cm dan tinggi 60 cm berisi air penuh. Sebuah bola berdiameter 21 cm dimasukkan ke dalam bak mandi sehingga air tumpah. Berapa volume air yang tersisa di dalam bak mandi?
Jawaban:
Diketahui:
Jari-jari tabung = (\(r_T\)) = 35/2 cm
Jari-jari bola = (\(r_B\)) = 21/2 cm
Tinggi tabung = (\(r_T\)) = 60 cm
Volume sisa air dalam tabung:
V = (\(V_{tabung}\)) – (\(V_{bola}\))
= π(\(r_T\)) (\(t_T\)) – (4/3)π(\(r_B\))³
= (22/7) × (35/2) × (35/2) × 60 – (4/3) × (22/7) × (21/2) × (21/2) × (21/2)
= 11 × 5 × 35 × 30 – 11 × 21 × 21
= 57.750 – 4.851
= 52.899 cm³
Jadi, volume air yang tersisa di dalam bak mandi adalah 52.899 cm³.
Pelajari Juga : Soal dan Penyelesaian Bangun Ruang Sisi Lengkung Kelas 9
Demikian “Soal Matematika Kelas 9 dan Kunci Jawaban“. Semoga Bermanfaat.