Barisan dan deret – Pada kesempatan ini saya akan memberikan 25 contoh soal dan pembahasan dari pola barisan dan deret kelas 9 SMP. Barisan bilangan dapat diartikan sebagai susunan bilangan yang memiliki keteraturan. Barisan bilangan terdiri dari:
1. Barisan bilangan asli
2. Barisan bilangan ganjil
3. Barisan bilangan kuadrat
4. Barisan bilangan segitiga
5. Barisan bilangan persegi panjang
6. Barisan bilangan segitiga pascal
Barisan aritmetika adalah barisan bilangan yang selisih antara dua suku barisan yang berurutan mempunyai nilai yang sama. Barisan geometri adalah barisan bilangan yang perbandingan setiap dua suku barisan berurutan nilainya selalu sama.
Untuk penjelasan singkat tentang pola barisan dan deret, Gengs dapat membuka link berikut:
Pada link tersebut juga diberikan beberapa soal latihan beserta pembahasannya.
Pada postingan kali ini, akan saya berikan 25 nomor soal tentang pola barisan dan deret. Semoga soal-soal tersebut dapat bermanfaat.
Soal 1
Tentukan tiga bilangan selanjutnya dari barisan bilangan
1, 4, 16, 64, 256, …
Jawab:
Barisan yang kita punya yaitu
1, 4, 16, 64, 256,…
Karena kita disuruh tentukan tiga bilangan selanjutnya, maka kita akan misalkan tiga bilangan tersebut dengan a, b dan c sebagai berikut.
1, 4, 16, 64, 256, a, b, c
Oleh karena,
Maka:
a = 256 x 4 = 1024
b = 1024 x 4 = 4096
c = 4096 x 4 = 16384
Dengan demikian, tiga bilangan selanjutnya adalah 1024, 4096 dan 16384.
Soal 2
Perhatikan barisan bilangan berikut ini!
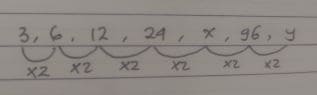
3, 6, 12, 24, x, 96, y
Nilai x dan y berturut-turut adalah…
Jawab:
Pertama-tama kita tentukan pola yang terbentuk dari barisan bilangan tersebut. Perhatikan gambar berikut.
Karena polanya telah kita peroleh, maka dengan mudah akan kita tentukan nilai x dan y.
x = 24 x 2 = 48
y = 96 x 2 = 192
Jadi nilai x dan y berturut-turut adalah 48 dan 192.
Soal 3
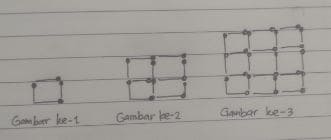
Perhatikan barisan gambar berikut.
Gambar di atas dibentuk dari batang-batang korek api. Jika Rima ingin membuat gambar ke-10, banyak batang korek api yang diperlukan … batang.
Jawab:
Mari kita perhatikan kembali gambar di atas.
Pada gambar ke-1 tersusun atas 4 batang korek api
Pada gambar ke-2 tersusun atas 12 batang korek api
Pada gambar ke-3 tersusun atas 24 batang korek api
Agar kita dapat mengetahui banyak korek api pada gambar ke-10, kita harus mengetahui pola yang terbentuk dari ketiga gambar tersebut.
Gambar ke-1 = 4 = 2(1²) + 2(1)
Gambar ke-2 = 12 = 2(2²) + 2(2)
Gambar ke-3 = 24 = 2(3²) + 2(3)
Dari ketiga pola yang telah kita tentukan maka pola gambar ke-n :
Gambar ke-n = 2(n²) + 2(n)
Dengan demikian pola gambar ke-10 adalah:
Gambar ke-10 = 2(10²) + 2(10)
= 2(100) + 20
= 200 + 20
= 220
Soal 4
Perhatikan gambar berikut ini!
Banyak noktah pada gambar ke-20 adalah…
Jawab:
Informasi yang kita peroleh dari gambar di atas yaitu:
Gambar ke-1 banyak noktah adalah 2
Gambar ke-2 banyak noktah adalah 6
Gambar ke-3 banyak noktah adalah 12
Gambar ke-4 banyak noktah adalah 20
Agar kita dapat mengetahui banyak noktah pada gambar ke-20, kita harus mengetahui pola yang dibentuk dari keempat gambar di atas.
Gambar ke-1 = 2 = 1² + 1
Gambar ke-2 = 6 = 2² + 2
Gambar ke-3 = 12 = 3² + 3
Gambar ke-4 = 20 = 4² + 4
Gambar ke-n = n² + n
Karena kita telah mengetahui pola yang dibentuk dengan mencari pola pada gambar ke-n maka dengan mudah kita akan tentukan banyak noktah pada gambar ke-20
Gambar ke-20 = 20² + 20
= 400 + 20
= 420
Soal 5
Jika diketahui rumus suku ke-n suatu barisan adalah n²- n, tentukan empat suku pertamanya!
Jawab:
Un = n² – n + = 27
Suku pertama = U₁ = 1² – 1 = 0
Suku kedua = U₂ = 2² – 2 = 2
Suku ketiga = U₃ = 3² – 3 = 6
Suku keempat = U₄ = 4² – 4 = 12
Jadi, empat suku pertama barisan tersebut yaitu 0, 2, 6, 12.
Soal 6
Diketahui Un = 2n² – 5. Nilai dari U₄ + U₅ adalah…
Jawab:
Karena Un = 2n² – 5
Maka kita dengan mudah menentukan U₄ dan U₅.
U₄ = 2(4²) – 5 = 2(16) – 5 = 32 – 5 =27
U₅ = 2(5²) – 5 = 2(25) – 5 = 50 – 5 = 45
Dengan demikian
U₄ + U₅ = 27 + 45 = 72
Soal 7
Rumus suku ke-n barisan bilangan 2,6,10,14,18,… adalah…
Jawab:
Suku ke-1 = U₁ = 2 = 2(2.1 – 1)
Suku ke-2 = U₂ = 6 = 2(2.2 – 1) =
Suku ke-3 = U₃ = 10 = 2(2.3 – 1)
Suku ke-4 = U₄ = 14 = 2(2.4 – 1)
Suku ke-5 = U₅ = 18 = 2(2.5 – 1) …
Dengan demikian,
Suku ke-n = Un = 2(2.n – 1) = 4n – 2
Soal 8
Perhatikan barisan bilangan berikut.
0, 3, 8, 15, 24, …
Bilangan 728 merupakan suku ke berapa dari barisan bilangan tersebut.
Jawab:
Suku ke-1 = U₁ = 0 = 1² – 1
Suku ke-2 = U₂ = 3 = 2² – 1
Suku ke-3 = U₃ = 8 = 3² – 1
Suku ke-4 = U₄ = 15 = 4² – 1
Suku ke-5 = U₅ = 24 = 5² – 1 …
Suku ke-n = Un = n² – 1
Bilangan 728 merupakan suku ke berapa?
Kita misalkan bilangan 728 merupakan suku ke-x maka:₀
Ux = x² – 1
728 = x² – 1
x² = 728 + 1
x² = 729
x = √(729) = 27
Jadi, bilangan 728 merupakan suku ke-27.
Soal 9
Diketahui barisan bilangan 4, 9, 14, 19, 24, … Besar suku ke-100 barisan bilangan tersebut adalah…
Jawab:
Suku ke-1 = U₁ = 4 = 4.1 + 0
Suku ke-2 = U₂ = 9 = 4.2 + 1
Suku ke-3 = U₃ = 14 = 4.3 + 2
Suku ke-4 = U₄ = 19 = 4.4 + 3
Suku ke-5 = U₅ = 24 = 4.5 + 4 …
Suku ke-n = Un = 4.n + (n-1) = 4n + n – 1 = 5n – 1
Karena Un = 5n – 1 maka
U₁₀₀ = 5(100) – 1 = 500 – 1 = 499
Soal 10
Perhatikan barisan bilangan berikut ini.
3, 7, 11, 15, …, 79, 83
Banyak suku pada barisan bilangan tersebut adalah…
Jawab:
Suku ke-1 = U₁ = 3
Suku ke-2 = U₂ = 7
Suku ke-3 = U₃ = 11
Suku ke-4 = U₄ = 15
Akan kita tentukan suku ke-n dari keempat informasi di atas dengan mencari polanya terlebih dahulu.
Suku ke-1 = U₁ = 3 = 3.1 + 1 – 1
Suku ke-2 = U₂ = 7 = 3.2 + 2 – 1
Suku ke-3 = U₃ = 11 = 3.3 + 3 – 1
Suku ke-4 = U₄ = 15 = 3.4 + 4 – 1
Suku ke-n = Un = 3.n + n – 1 = 4n – 1
Karena kita belum mengetahi berapa banyak suku dari barisan tersebut, maka kita misalkan bilangan 83 merupakan suku ke-n. Dengan demikian kita dapat menentukan banyak suku (n) pada barisan bilangan tersebut.
Un = 83
4n – 1 = 83
4n = 84
n = 21
Jadi, banyak suku pada barisan tersebut adalah 21.
Soal 11
Tentukan rumus suku ke-n pada barisan aritmetika 10, 18, 26, 34,…
Jawab:
Pertama-tama yang perlu kita lakukan yaitu mencari suku pertama dan beda.
Dari soal dapat kita ketahui suku satu (a) adalah 10
Beda = suku ke dua – suku ke satu
= 18 – 10 = 8
Selanjutnya, dengan mudah akan kita tentukan suku ke-n
Un = a + (n – 1)b
= 10 + (n – 1)8
= 10 + 8n – 8
= 8n + 2
Soal 12
Tentukan jumlah deret aritmetika berikut.
10 + 17 + 24 + 31 + … + 115
Jawab:
Dari soal akan kita peroleh:
U₁ = a = 10
Karena barisan tersebut barisan aritmetika maka selisih antara dua suku barisan yang berurutan mempunyai nilai yang selalu tetap atau sama.
b = U₂ – U₁ = 17 – 10 = 7
Un = 115
Sedangkan, kita diperintahkan untuk mencari jumlah dari deret tersebut.
Namun, sebelumnya kita harus mencari berapa banyak suku pada barisan tersebut.
Un = a + (n – 1)b
115 = 10 + (n – 1)7
115 = 10 + 7n – 7
115 = 7n + 3
7n = 112
n = 16
Setelah kita dapatkan nilai n, selanjutnya kita cari jumlah deret tersebut.
Sn = (n/2) (U₁ + Un)
= (16/2) (10 + 115)
= (8)(125) = 1000
Jadi, jumlah deret aritmetika tersebut adalah 1000.
Soal 13
Diketahui suatu barisan aritmetika dengan U₂ = 6 dan U₇ = 31. Suku ke-40 adalah…
Jawab:
Un = a + (n – 1)b
U₂ = a + (2 – 1)b
6 = a + b
a = 6 – b …. Pers 1
U₇ = a + (7 – 1)b
31 = a + 7b – b
31 = a + 6b … Pers 2
Substitusi pers 1 ke dalam pers 2
a + 6b = 31
(6 – b) + 6b = 31
6 + 5b = 31
5b = 25
b = 5
Substitusi b = 5 ke dalam pers 1
a = 6 – b
a = 6 – 5
a = 1
Seanjutnya kita cari U₄₀ dengan mensubstitusi a = 1 dan b = 5 ke dalan U₄₀ = a + 39b.
U₄₀ = a + 39b
= 1 + 39(5)
= 1 + 195 = 196
Jadi, suku ke-40 adalah 196.
Soal 14
Diketahui barisan aritmetika dengan U₁ = 3 dan U₈ = 24. Beda pada barisan aritmetika tersebut adalah…
Jawab:
U₁ = 3
a = 3
U₈ = 24
a + (n – 1)b = 24
3 + (8 – 1)b = 24
3 + 7b = 24
7b = 21
b = 3
Jadi, beda pada barisan aritmetika tersebut adalah 3.
Soal 15
Jika rumus suku ke-n barisan aritmetika Un = 4n – 5, beda pada barisan tersebut adalah…
Jawab:
Un = 4n – 5
Beda = Un – Un₋₁
Karena Un = 4n – 5
Maka Un₋₁= 4(n-1) – 5 = 4n – 4 – 5 = 4n – 9 –
Dengan demikian
Beda = (4n – 5) – (4n – 9)
= 4n – 5 – 4n + 9
= 4
Jadi, beda pada barisan tersebut adalah 4.
Soal 16
Diketahui deret aritmetika berikut.
(-10) + (-5) + 0 + 5 + … + 130
Banyak suku pada deret aritmetika tersebut adalah…
Jawab:
U₁ = a = -10
b = U₂ – U₁ = (-5) – (-10) = -5 + 10 = 5
Un = a + (n – 1)b
Karena Un = 130 maka:
130 = (-10) + (n – 1)5
130 = (-10) + 5n – 5
130 = 5n – 15
5n = 145
n = 29
Jadi, banyak suku pada deret aritmetika tersebut adalah 29.
Soal 17
Jika rumus jumlah n suku pertama suatu deret aritmetika Sn = 3n² – n, maka suku ke-25 adalah…
Jawab:
Un = a + (n – 1)b
U₂₅ = a + (25 – 1)b = a + 24b
a = U₁ = S₁
b = U₂ – U₁
Untuk mencari U₂₅, kita cari lebih dahulu S₁ dan b.
Mencari S₁
Sn = 3n² – n
S₁ = 3.1² – 1 = 3 – 1 = 2
Mencari b
b = U₂ – U₁
U₁ = S₁ = 2
U₂ = S₂ – S₁
Sn = 3n² – n
S₂ = 3.2² – 2 = 12 – 2 = 10
U₂ = S₂ – S₁ = 10 – 2 = 8
b = U₂ – U₁ = 8 – 2 = 6
Dengan demikian,
U₂₅ = a + 24b
= 2 + 24(6)
= 2 + 144 = 146
Soal 18
Jika diketahui 8 + 17 + 26 + … = 690, banyaknya bilangan dari deret tersebut adalah…
Jawab:
U₁ = a = 8
U₂ = 17
U₃ = 26
b = 17 – 8 = 9
Sn = 690
Banyak bilangan (n) :
Sn = (n/2) [2a + (n-1)b]
690 = (n/2) [2(8) + (n – 1)9]
690 = (n/2) [16 + 9n – 9]
1380 = n [9n + 7]
1380 = 9n² + 7n
9n² + 7n – 1380 = 0
Dengan menggunakan rumus ABC akan diperoleh n = 12.
Soal 19
Diketahui barisan bilangan 1, 12, 23, 34, 45, … Suku ke-100 barisan tersebut adalah…
Jawab:
U₁ = a = 1
U₂ = 12
b = U₂ – U₁ = 12 – 1 = 11
Un = a + (n – 1)b
U₁₀₀ = 1 + (100 – 1)11
= 1 + 99(11)
= 1 + 1089 = 1090
Jadi, suku ke-100 barisan tersebut adalah 1090.
Soal 20
Diketahui barisan berikut.
7, 21, 63, 189, …
Tentukanlah barisan bilangan yang termasuk barisan geometri.
Jawab:
Pertama, mari kita cari perbandingan setiap dua suku berurut.
Oleh karena perbandingan setiap dua suku yang berurutan besarnya tetap yaitu 3, maka barisan 7, 21, 63, 189, … merupakan barisan geometri.
Soal 21
Perhatikan barisan geometri berikut ini.
2, 6, 18, 54, 162, …
Rasio barisan geometri tersebut adalah…
Jawab:
U₁ = 2
U₂ = 6
U₃ = 18 =
U₄ = 54
U₅ = 162
r = Un/Un₋₁ = U₂/U₁ = U₃/U₂ = U₄/U₃= U₅/U₄
r = 6/2 = 18/6 = 54/18 = 162/54 = 3
Jadi, rasio barisan geometri tersebut adalah 3.
Soal 22
Perhatikan barisan berikut.
5, 10, 20, 40, x, 160, y, …
Nilai x dan y berturut-turut adalah…
Jawab:
Pertama-tama, mari kita cari rasio (r)
r = Un/Un-1
Karena U₁=a=5 U₂=10 U₃=20 U₄=40 U₅=x U₆=160 U₇=y maka:
r = U₂/U₁ = 10/5 = 2
Cari nilai x
Un = arⁿ⁻¹
U₅ = x
ar⁴ = x
(5)(2⁴) = x
(5)(16) = x
x = 80
Cari nilai y
Un = arⁿ⁻¹
U₇ = y
ar⁶ = y
(5)(2⁶) = y
(5)(64) = y
y = 320
Jadi nilai x = 80 dan y = 320
Soal 23
Nilai suku ke delapan dari barisan geometri 4, 12, 36, 108, … adalah…
Jawab:
Suku pertama = U₁ = a = 4
Suku kedua = U₂ = 12
Suku ketiga = U₃ = 36
Suku keempat = U₄ = 108 =
r = U₂/U₁ = U₃/U₂ = U₄/U₃
r = 12/4 = 36/12 = 108/36 = 3
Nilai suku kedelapan:
Un = arⁿ⁻¹
U₈ = (4)(3⁷)
= (4)(2187) =8748
Jadi, nilai suku ke delapan adalah 8748.
Soal 24
Diketahui deret geometri 6 + 12 + 24 + 48 + … Jumlah 10 suku pertama deret tersebut adalah…
Jawab:
Suku pertama = U₁ = 6
Suku kedua = U₂ = 12
Suku ketiga = U₃ = 24
Suku keempat = U₄ = 48
Rasio = r = U₂/U₁ = 12/6 = 2
Jumlah 10 suku pertama:
Sn = a (rⁿ – 1) / r – 1
S₁₀ = 6 (2¹⁰ – 1) / 2 – 1
= 6(1024 – 1) / 1
= 6 (1023)
= 6138
Jadi, jumlah 10 suku pertama deret tersebut adalah 6138
Soal 25
Pada suatu barisan geometri diketahui U₁ = 15 dan U₃ = 135. Nilai suku ke-5 adalah…
Jawab:
U₁ = 15 = a
U₃= 135
a r² = 135
(15) (r²) = 135
r² = 135/15 = 9
r = √9 = 3
Nilai suku ke-5:
Karena a = 15 dan r = 3 maka,
U₅ = a r⁴
= (15) (3⁴)
= (15) ( 81) = 1215
Jadi, nilai suku ke-5 adalah 1215.
Untuk mempermudah mengerjakan soal-soal latihan, jangan lupa mempelajari materinya terlebih dahulu.
2 komentar di “25 Contoh Soal dan Pembahasan Pola Barisan dan Deret Kelas 9”
Tinggalkan Balasan
Anda harus masuk untuk berkomentar.



I blog often and І seriously appreciate your content. This article has truly
peaked mʏ interest. І am going to boоkmark your site and keep checking for new information about once per week.
І opted in for your Feed as well.
Thank you