Haiii Gengs, bagaimana keadaan kalian hari ini? Pada kesempatan kali ini saya akan memposting contoh soal dan penyelesaian tentang bangun ruang sisi lengkung. Materi ini dipelajari pada jenjang SMP lebih tepatnya kelas 9. Saya hanya akan memposting 8 nomor soal latihan, Gengs bisa banyak berlatih lagi soal-soal yang disediakan dalam buku paket.
Soal 1
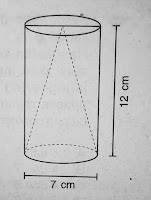
Sebuah kerucut berada di dalam tabung seperti gambar di bawah ini.
Volume tabung di luar kerucut adalah…
Jawab:
Volume tabung
V= π x r² x t
V₁=22/7×7/2×7/2×12
=11×7×6
=462 cm³
Volume kerucut
V=1/3 x π x r² x t
V₂=1/3×22/7×7/2×7/2×12
=11×7×2
=154 cm³
Volume tabung di luar kerucut yaitu:
V=V₁ (tabung) – V₂ (kerucut)
= 462 – 154
= 308 cm³
Dengan demikian, volume tabung di luar kerucut adalah 308 cm³
Soal 2
Dua bola dimasukkan ke dalam tabung. Jika panjang jari-jari bola 10 cm, luas permukaan tabung adalah…
Jawab:
Jari-jari tabung sama dengan jari-jari bola yaitu 10 cm [r=10 cm].
Tinggi tabung sama dengan dua kali diameter yaitu:
t=2x2x10=40 cm
Luas permukaan tabung yaitu:
L=2 x π x r²+ 2 x π x r x t
= 2πr(r+t)
= 2π(10)(10+40)
= 2π(10) (50)
= 1000π cm²
Jadi, luas permukaan tabung adalah 1000π cm²
Soal 3
Sebuah kerucut mempunyai volume 10 cm³. Diameter kerucut tersebut diperbesar dua kali dan tingginya diperbesar tiga kali. Volume kerucut yang baru adalah…
Jawab:
Kerucut mempunyai volume 10 cm³ maka:
V kerucut = 1/3 x π x r² x t = 10
π x r² x t = 30
Karena kerucut yang baru diperbesar dua kali (2r) dan tinggi diperbesar tiga kali (3t) maka:
V = 1/3 x π x (2r)² x 3t
= 1/3 x π x 4r² x 3t
= 4πr² t
= 4(30)
= 120 cm³
Jadi, volume kerucut yang baru adalah 120 cm³
Soal 4
Perhatikan gambar kerucut dan tabung di bawah ini.
Volume bangun tersebut adalah…
Jawab:
Volume tabung
Tabung dengan tinggi (t) = 9 cm dan diameter (d) = 10 cm, maka jari-jari (r) = 5 cm.
V tabung = π x r² x t
= π x 5² x 9
= 225π cm³
Volume kerucut
Untuk mencari volume kerucut, Gengs perhatikan gambar di bawah ini.
Kerucut dengan jari-jari (r) = 5 cm.
Tinggi kerucut yaitu:
Volume kerucut=1/3 x π x r² x t
= 1/3 x π x 5² x 12
= 100π cm³
Volume = Volume tabung + Volume kerucut
= 225π + 100π
= 325π cm³
Jadi, volume bangun tersebut adalah 325π cm³
Soal 5
Perhatikan gambar di bawah ini!
Luas permukaan bangun tersebut adalah…
Jawab:
Permukaan bangun tersebut terdiri atas lingkaran, selimut tabung dan selimut kerucut.
Lingkaran
Lingkaran dengan diameter (d) = 14 cm sehingga jari-jari (r) = ½ x 14 = 7 cm
Luas lingkaran = π x r²
= (22/7) x 7²
=154 cm²
Selimut tabung
Selimut tabung dengan diameter (d) = 14 cm dan tinggi (t) = 10 cm
Luas selimut tabung =2 x π x r x t
= 2 x (22/7) x 7 x 10
= 2 x 22 x 10
= 440 cm²
Selimut kerucut
Selimut kerucut dengan diameter (d) = 14 cm dan tinggi (t) = 24 cm maka panjang garis pelukis yaitu:
√s= r² + t²
= 7² + 24²
= 49 + 576
= 625
s = 25 cm
Luas selimut kerucut = π x r x s
= (22/7) x 7 x 25
= 550 cm²
Luas permukaan bangun secara keseluruhan = luas lingkaran + luas selimut tabung + luas selimut kerucut
L = 154 + 440 + 550
= 1.144 cm²
Jadi, luas permukaan bangun tersebut adalah 1.144 cm²
Soal 6
Sebuah kerucut mempunyai diameter alas 14 cm dan tinggi 24 cm. Luas permukaan kerucut tersebut adalah…
Jawab:
Kerucut disajikan seperti gambar di bawah ini.
Panjang diameter (QR) = 14 cm maka jari-jari (OR) = 7 cm.
Panjang garis pelukis yaitu:
√PR=PO² + OR²
= 24² + 7²
= 576 + 49
= 625
PR = 25 cm
Luas permukaan kerucut = Luas alas + Luas selimut
L = π r² + πr s
= π r (r + s)
= (22/7) x 7 (7 + 25)
= 22(32)
= 704 cm²
Jadi, luas permukaan kerucut tersebut adalah 704 cm²
Soal 7
Volume bola terbesar yang dapat dimasukan ke dalam sebuah kubus dengan panjang rusuk 24 cm adalah…
Jawab:
Volume bola terbesar yang dapat dimasukkan yaitu berdiameter (d) = 24 cm maka jari-jari (r) = 12 cm
Volume bola terbesar = (4/3) x π x r³
= (4/3) x π x 12³
= 2.304 cm³
Jadi, volume bola terbesar yang dapat dimasukkan dalam sebuah kubus yaitu 2.304 cm³
Soal 8
Perhatikan gambar berikut ini!
Bangun di atas tersusun atas dua bagian. Pada bagian atas berbentuk kerucut dan bagian bawah berbentuk setengan bola. Volume bangun gabungan tersebut adalah…
Jawab:
Bagian bawah (setengan bola)
Diameter bola (d) = 14 cm sehingga jari-jari (r) = 7 cm
Volume setengah bola sebagai berikut:
V₁ = (1/2) x (4/3) x π x r³
= (1/2) x (4/3) x (22/7) x 7³
= 2156/3 cm³
Bagian atas (kerucut)
Jari-jari (r) kerucut = 7cm dan tinggi (t) kerucut = 17-7=10 cm maka volume kerucut yaitu:
V₂ = (1/3) x π x r² x t
= (1/3) x (22/7) x 7² x 10
= 1.540/3 cm³
Volume gabungan bangun tersebut yaitu:
V = V₁ + V₂
= (2156/3) + (1540/3)
= 3.696/3
= 1.232 cm³
Jadi, Volume gabungan bangun tersebut yaitu 1.232 cm³.
Demikian contoh-contohnya. Apabila ada kesalahan, mohon di kritik. Semoga Bermanfaat