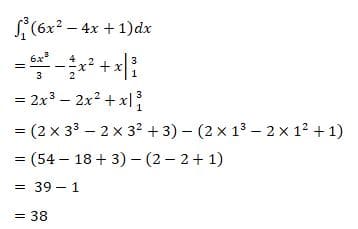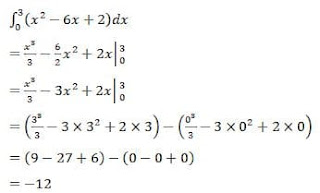Berikut ini saya berikan 30 soal latihan Ujian Sekolah (US) matematika SMA dan penyelesaiannya.
Tanpa basa-basi berikut 30 soal latihan US matematika SMA.
Soal 1
Bentuk sederhana dari (2a³ b⁻² )⁴/(2a⁻⁴ b⁻⁵)⁻² adalah…
Penyelesaian:
(2a³ b⁻² )⁴/(2a⁻⁴ b⁻⁵ )⁻²
=(2⁴ (a³ )⁴ (b⁻² )⁴)/(2⁻² (a⁻⁴)⁻² (b⁻⁵)⁻²)
=(2⁴ a¹² b⁻⁸)/(2⁻² a⁸ b¹⁰ )
=2⁴⁻⁽⁻²⁾ a¹²⁻⁸ b⁻⁸⁻¹⁰
=2⁶ a⁴ b⁻¹⁸
=(2⁶ a⁴)/b¹⁸
Soal 2
Himpunan penyelesaian dari persamaan 2³ˣ⁻²=32ˣ⁻⁴ adalah…
Penyelesaian:
2³ˣ⁻²=32ˣ⁻⁴
2³ˣ⁻²=(2⁵)ˣ⁻⁴
2³ˣ⁻²=2⁵ˣ⁻²⁰
3x-2=5x-20
3x-5x=-20+2
-2x=-18
x=9
Jadi, HP={9}
Soal 3
Himpunan penyelesaian dari sistem persamaan linear 7x+3y=-5 dan 5x+2y=1 adalah…
Penyelesaian:
Menggunakan metode substitusi dan eliminasi.
7x+3y=-5 |x2|14x+ 6y=-10
5x+2y=1 |x3|15x+6y=3
———————- –
-x= -13
x=13
5x+2y = 1
5(13) + 2y = 1
65+2y=1
2y=-64
y=-32
Jadi, himpunan penyelesaian dari SPL tersebut yaitu {13,-32}.
Soal 4
Andi membeli 2 buku tulis dan 3 pensil dengan harga Rp 8.500 sedangkan Didit membeli 3 buku tulis dan 2 pensil dengan harga Rp 9.000. Harga 1 buku dan 1 pensil adalah…
Penyelesaian:
Misalkan:
x=buku tulis
y=pensil
Diketahui:
2x+3y=8.500
3x+2y=9.000
Dengan metode eliminasi dan substitusi diperoleh:
2x+3y=8.500|x2|4x+6y=17.000
3x+2y=9.000|x3|9x+6y=27.000
——————– –
-5x = -10.000
x = 2.000
Substitusikan x=2.000 ke dalam persamaan 3x+2y=9.000
3x+2y=9.000
3(2.000)+2y=9.000
6.000+2y=9.000
2y=3.000
y=1.500
Karena x adalah buku tulis dan y adalah pensil maka harga 1 buku tulis yaitu Rp 2.000 dan harga 1 pensil yaitu Rp 1.500.
Soal 5
Diketahui cos A=12/13 dengan 270°≤A≤360°. Nilai tan A adalah…
Penyelesaian:
Diketahui:
cos A = 12/13 = x/r
Ditanya: tan A =….?
tan A = -(y/x) (negatif karena berada di kuadran iv)
x telah diketahui, akan kita cari y.
13²= 12²+y²
13²-12²=y²
169-144=y²
25=y²
y=5
Dengan demikian, tan A= -(y/x) = -(5/12)
Soal 6
Diketahui matriks \(A=\left (\begin{matrix}4 &-6 &1 \\2 &3 &-2 \end{matrix} \right )\) dan \(B=\left (\begin{matrix}3 \\0 \\-1\end{matrix} \right )\). Hasil AB adalah…
Penyelesaian:
Soal 7
Invers matriks \(A=\left (\begin{matrix}-4 &-1 \\6 &2 \end{matrix} \right )\) adalah…
Penyelesaian:
Diketahui:
\(A=\left (\begin{matrix}-4 &-1 \\6 &2 \end{matrix} \right )\)
Dengan, a=-4, b=-1, c=6 dan d=2 maka:
det A = ad-bc =(-4 ⨯ 2) – (-1 ⨯ 6) = -8 – (-6) = -8+6 = -2
Dengan demikian,
Soal 8
Akar-akar persamaan kuadrat x²-8x+16=0 adalah…
Penyelesaian:
x²-8x+16=0
(x-4)(x-4)=0
(x-4)²=0
x-4=0
x=4
Jadi, akar persamaan kuadratnya yaitu x=4.
Soal 9
Diketahui komponen \(\vec{a}=\left (\begin{matrix}-6 \\8 \end{matrix} \right )\), maka \(\left|\vec{a} \right|\) adalah…
Penyelesaian:
\(\vec{a}=\left (\begin{matrix}-6 \\8 \end{matrix} \right )\) dengan a₁=-6 dan a₂=8.
\(\left|\vec{a} \right|\) = panjang vektor
Dengan demikian, \(\left|\vec{a} \right|\)=10
Soal 10
Diketahui premis-premis berikut ini!
Premis 1: Jika harga minyak naik maka harga barang ikut naik.
Premis 2: Jika harga barang ikut naik maka banyak pengusaha rugi.
Kesimpulan dari premis-premis di atas adalah…
Penyelesaian
Dengan aturan silogisme dapat kita peroleh:
p \(\rightarrow\) q (premis 1)
q \(\rightarrow\) r (premis 2)
Kesimpulan: p \(\rightarrow\) 5 (konklusi)
Kesimpunanya yaitu jika harga minyak naik maka banyak pengusaha rugi.
Soal 11
Ingkaran dari pernyataan “Jika semua siswa mengikuti upacara, maka guru akan senang” adalah…
Penyelesaian:
Ditanyakan ingkaran dari pernyataan tersebut.
Misalkan:
p=semua siswa mengikuti upacara
q=guru akan senang
Premis= Jika semua siswa mengikuti upacara, maka guru akan senang.
= p \(\rightarrow\) q
INGAT!
Ingkaran dari “semua” adalah “ada” atau “beberapa”.
Dengan demikian ingkaran dari pernyataan tersebut yaitu:
Jika beberapa siswa mengikuti upacara maka guru tidak akan senang.
Soal 12
Pada pelemparan 2 buah mata uang logam, peluang muncul dua sisi yang sama adalah…
Penyelesaian:
S={AA,AG,GA,GG}
n(S)=4
N(k)=2
P(A)=n(k)/n(S) = 2/4=1/2
Jadi, peluang muncul 2 sisi uang sama yaitu ½.
Soal 13
Bayangan titik P(6,-2) oleh translasi \(\left (\begin{matrix}4 \\2 \end{matrix} \right )\) adalah…
Penyelesaian:
Translasi = pergeseran
INGAT!
Jika titik P(a,b) ditranslasi dengan \(T=\left (\begin{matrix}h k\end{matrix} \right )\) maka bayangannya adalah titik P’. Koordinat P’ yaitu P(a,b) \(\rightarrow\) P’(a+h,b+k)
Dengan demikian,
P’(6,-2) \(\rightarrow\) P’(6+4,-2+2)
\(\rightarrow\) P'(10,0)
Soal 14
Titik A(8,-2) dicerminkan terhadap garis y=-x. Koordinat bayangan titik A adalah…
Penyelesaian:
INGAT!
Pencerminan terhadap garis y = -x
A(x,y) \(\rightarrow\) A’(-y,-x)
Dengan demikian
A(8,-2) \(\rightarrow\) A’(2,-8)
Soal 15
Perhatikan daftar distribusi frekuensi data berikut.
Median dari data di atas adalah…
Penyelesaian:
Median adalah nilai tengah dari data yang telah disusun berurutan mulai dari data yang terkecil sampai terbesar.
RUMUS
Median untuk data genap:
Me=1/2 (\(X_{n/2}\) + \(X_{n/2 +1}\))
Median untuk data ganjil:
Me=\(X_{(n+1)/2}\)
Dari soal di atas jumlah data adalah 2+3+5+5+8+3+4=30 (genap), maka:
Me = 1/2 (\(X_{n/2}\) + \(X_{n/2 +1}\))
= ½ (\(X_{30/2}\) + \(X_{30/2+1}\))
= ½(X₁₅ + X₁₆)
X₁₅ yaitu data ke-15 setelah diurutkan.
X₁₅=7
X₁₆ yaitu data ke-16 setelah diurutkan
X₁₆=8
Dengan demikian,
Me = ½(7+8) = ½(15) = 7,5
Soal 16
Simpangan kuartil dari data: 5,2,9,12,4,6,9,10,5 adalah…
Penyelesaian:
Rumus!
Simpangan kuartil: ½ (Q₃- Q₁)
Banyak data (n) = 9 (ganjil)
Merncari Q₁ dan Q₃
Q₁ = ¼ (n+1) = ¼ (9+1) = ¼ (10) = 10/4 = 2,5 (artinya terletak diantar data ke-2 dan ke-3)
Q₁ = (4+5)/2=4,5
Q₃ = ¾ (n+1) = ¾ (9+1) = ¾ (10) = 30/4 = 7,5 (artinya terletak diantara data ke-7 dan ke-8)
Q₃ = (9+10)/2 = 19/2 = 8,5
Dengan demikian,
Simpangan kuartil = ½ (8,5 – 4,5) = ½(4) = 2
Soal 17
Perhatikan daftar distribusi frekuensi data berkelompok berikut.
Median dari data pada tabel di atas adalah…
Penyelesaian:
Letak Me atau Q₂ = ½ (n+1) = ½ (40+1) = 20,5 (di kelas 3)
Kelas Q₂ adalah 52-57
Maka:
bm = 51,5
n=40
fk=9
fq₂ = 12
c = 57 – 52 = 5
Dengan demikian,
Soal 18
Simpangan baku dari data 3,7,4,6,5,2,8 adalah…
Penyelesaian:
Data setelah diurutkan: 2,3,4,5,6,7,8
Simpangan baku = √Ragam
Ragam=\(\frac{1}{n}\sum_{i=1}^{r}f\left ( x_{i}-x \right )\)
Diperoleh dari soal: n = 7
\(\bar{x}=\frac{2+3+4+5+6+7+8}{7}=\frac{35}{7}=5\)
Ragam=1/7 ((2-5)+(3-5)+(4-5)+(5-5)+(6-5)+(7-5)+(8-5))
=1/7 ((-3)+(-2)+(-1)+0+1+2+3)
=1/7 (0)
=0
Dengan demikian,
Simpangan baku=√Ragam=√0=0
Soal 19
Diketahui data: 24,15,13,20,22,7,17,18. Simpangan rata-rata dari data tersebut adalah…
Penyelesaian:
Data setelah diurutkan: 7,13,15,17,18,20,22,24
Simpangan rata-rata=\(\frac{1}{n}\sum_{i=1}^{r}\left|x_{i}-\bar{x} \right|\)
Diketahui:
n=8
\(\bar{x}\)=(7+13+15+17+18+20+22+24)/8=136/8=17
Dengan demikian,
SR=1/8 (|7-17|+|13-17|+|15-17|+|17-17|+|18-17|+|20-17|+|22-17|+|24-17|)
=1/8 (10+4+2+0+1+3+5)
=1/8 (32)
=4
Soal 20
Nilai dari \(\displaystyle \lim_{x \to 0}\frac{2x^{5}+9x^{3}-4x}{2x-3x^{2}-7x^{5}}\) adalah…
Penyelesaian:
Karena apabila kita substitusikan x=6 hasilnya 0/0 maka akan kita kerjakan seperti berikut:
Soal 21
Nilai dari \(\displaystyle \lim_{x \to 6}\frac{x-6}{x^{2}-4x-12}\) adalah…
Penyelesaian:
Karena apabila kita substitusikan x=6 hasilnya 0/0 maka akan kita kerjakan seperti berikut:
\(\displaystyle \lim_{x \to 6}\frac{x-6}{x^{2}-4x-12}\)
\(=\displaystyle \lim_{x \to 6}\frac{x-6}{(x-6)(x+2)}\)
\(=\displaystyle \lim_{x \to 6}\frac{1}{x+2}\)
\(=\frac{1}{6+2}\)
\(=\frac{1}{8}\)
Soal 22
Turunan pertama dari f(x) = 3x (4x²-2x) adalah…
Penyelesaian:
f(x) = 3x (4x²-2x) = 12x³-6x²
f’(x)=12(3)x² – 6(2)x = 36x² – 12x
Soal 23
Turunan pertama dari fungsi y = (3x²-2)/(2x+1) untuk x#-1/2 adalah…
Penyelesaian:
y=(3x²-2)/(2x+1)
Misalkan:
u=3x²-2 ⇒ u’=6x
v=2x+1 ⇒ v’=2
y´=(u´v – uv´)/v²
=((6x)(2x+1)-(3x²-2)(2))/(2x+1)²
=((12x²+6x)-(6x²-4))/(4x²+4x+1)
=(6x²+6x+4)/(4x²+4x+1)
Soal 24
Tentukan nilai dari ∫5x³(2x²+3x-1)dx
Penyelesaian:
∫5x³(2x²+3x-1)dx
=∫10x⁵+15x⁴-5x³)dx
=10/6 x⁶+15/5 x⁵-5/4 x⁴+C
=5/3 x⁶+3x⁵-5/4 x⁴+C
Soal 25
Tentukan \(\int_{1}^{3}\left ( 6x^{2}-4x+1 \right )dx\)
Penyelesaian:
Soal 26
Tentukan himpunan penyelesaian dari sistem persamaan linear 2x+3y=3 dan 3x-y=10
Penyelesaian:
2x+3y=3……..(1)
3x-y=10………(2)
Dari (2) diperoleh:
3x-y=10
-y=10-3x
y=3x-10…….(3)
Substitusikan (3) ke dalam (1)
2x+3y=3
2x+3(3x-10)=3
2x+9x-30=3
11x=33
x=3
Substitusikan x=3 ke dalam (3)
y=3x-10
y=3(3)-10=9-10=-1
Dengan demikian, himpunan penyelesaiannya yaitu {3,-1}.
Soal 27
Jika diketahui nilai rata-rata dari data 5,6,6,2,x,17,16,4 adalah 6,5. Tentukan:
a. Nilai x
b. Median dan Modus
Penyelesaian:
Data: 5,6,6,2,x,17,16,4
Nilai rata-rata = 6,5
n = 8
a. Mencari nilai x
x = (5+6+6+2+x+17+16+4)/8
6,5 = (56+x)/8
8(6,5) = 56+x
52 = 56+x
x = -4
b. Mencari Median dan Modus
Median
Karena n = 8 (genap)
Akan kita gunakan rumus:
Me = ½ (\(x_{n/2}\) + \(x_{(n/2) + 1}\))
Data setelah diurutkan: -4,2,4,5,6,6,16,17
Maka,
Me = ½ (\(x_{8/2}\) + \(x_{8/2 + 1}\))
= ½ (x₄ + x₅)
= ½ (5+6) = 5,5
Modus
Modus yaitu nilai/data yang sering/paling banyak muncul.
Data: -4,2,4,5,6,6,16,17
Dari data tersebut, angka 6 muncul sebanyak 2 kali dengan demikian modus dari data tersebut yaitu 6.
Soal 28
Jika f’(x) adalah turunan pertama dari f(x)=2x³+7x²-8x-1, maka tentukan nilai dari f’(-1)?
Penyelesaian:
f(x)=2x³+7x²-8x-1
f’(x) = 6x²+14x-8
f’(-1) = 6(-1)²+14(-1)-8 = 6-14-8=-16
Soal 29
Luas daerah yang diarsir pada gambar di bawah ini adalah…
Penyelesaian:
Soal 30
Diketahui koordinat kutub titik P(6,300°). Koordinat Cartesius titik P adalah…
Penyelesaian:
Koordinat kutub (r,θ) = (6,300°)
x= r cos θ
= 6 cos 300°
=6 cos 60°
= 6 (1/2)
= 3
y=r sin θ
= 6 sin 300°
= 6 sin 60°
= 6 (-1/2 √3)
= -3 √3
Demikian “30 Soal Latihan Ujian Sekolah Matematika SMA dan Penyelesaiannya“. Semoga Bermanfaat.


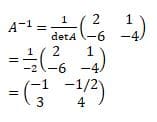

.jpg)


.jpg)