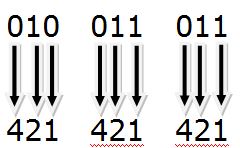
Kedua: Karena pada kelompok pertama (paling kiri) hanya memiliki 2 digit, maka tambahkan 0 pada kelompok pertama sebelum angka 1.
Ketiga: Tambahkan angka 4, 2, atau 1 di bawah masing-masing digit pada kelompok tiga angka sebagai penanda. Tiap angka dalam tiga angka biner memiliki nilai tempat di dalam sistem bilangan oktal. Angka pertama bernilai 4, yang kedua bernilai 2, dan yang ketiga 1.
Keempat: Jika ada angka satu di atas nilai tempat tadi, tuliskan nilai tempat (4, 2, atau 1) untuk mulai mencari angka oktal. Jika ada angka satu di atas 4, maka angka tersebut bernilai 4 dalam angka oktal. Jika ada angka nol di atas angka mana pun, nilai oktalnya nol.
Kelima: Tambahkan setiap angka yang baru diperoleh dari kelompok tiga angka. Begitu Anda mendapatkan nilai tempat di dalam bilangan oktal, tambahkan saja ketiganya.
Keenam: Masukkan semua angka yang diperoleh menjadi jawaban konversi nilai oktal. Setelah dikonversi, gabungkan semua angka kembali menjadi jawaban akhir.
Ketujuh: Tambahkan subskrip 8 untuk menyelesaikan konversi. Kita tidak bisa menentukan apakah angka 233 adalah sebuah bilangan oktal atau bilangan desimal berbasis sepuluh tanpa notasi yang tepat. Jadi, untuk memastikan pekerjaan Geng sudah dikerjakan dengan benar, tandai jawaban dengan subskrip 8, yang mengacu pada sistem oktal berbasis delapan.
233= \(233_8\)
CONTOH 2: 11001101
Kedua: Karena pada kelompok pertama (paling kiri) hanya memiliki 2 digit, maka tambahkan 0 pada kelompok pertama sebelum angka 1.
Ketiga: Tambahkan angka 4, 2, atau 1 di bawah masing-masing digit pada kelompok tiga angka sebagai penanda. Tiap angka dalam tiga angka biner memiliki nilai tempat di dalam sistem bilangan oktal. Angka pertama bernilai 4, yang kedua bernilai 2, dan yang ketiga 1.
Keempat: Jika ada angka satu di atas nilai tempat tadi, tuliskan nilai tempat (4, 2, atau 1) untuk mulai mencari angka oktal. Jika ada angka satu di atas “4”, maka angka tersebut bernilai 4 dalam angka oktal. Jika ada angka nol di atas angka mana pun, nilai oktalnya nol.
Kelima: Tambahkan setiap angka yang baru diperoleh dari kelompok tiga angka. Begitu Anda mendapatkan nilai tempat di dalam bilangan oktal, tambahkan saja ketiganya.
Keenam: Masukkan semua angka yang diperoleh menjadi jawaban konversi nilai oktal. Setelah dikonversi, gabungkan semua angka kembali menjadi jawaban akhir .
(0+2+1) (0+0+1) (4+0+1) = 3,1,5 = 315
315= \(315_8\)
CONTOH 3: 10110
Kedua: Karena pada kelompok pertama (paling kiri) hanya memiliki 2 digit, maka tambahkan 0 pada kelompok pertama sebelum angka 1.
Ketiga: Tambahkan angka 4, 2, atau 1 di bawah masing-masing digit pada kelompok tiga angka sebagai penanda. Tiap angka dalam tiga angka biner memiliki nilai tempat di dalam sistem bilangan oktal. Angka pertama bernilai 4, yang kedua bernilai 2, dan yang ketiga 1.
Keempat: Jika ada angka satu di atas nilai tempat tadi, tuliskan nilai tempat (4, 2, atau 1) untuk mulai mencari angka oktal. Jika ada angka satu di atas 4, maka angka tersebut bernilai 4 dalam angka oktal. Jika ada angka nol di atas angka mana pun, nilai oktalnya nol.
Kelima: Tambahkan setiap angka yang baru diperoleh dari kelompok tiga angka. Begitu Gengs mendapatkan nilai tempat di dalam bilangan oktal, tambahkan saja ketiganya.
Keenam: Masukkan semua angka yang diperoleh menjadi jawaban konversi nilai oktal. Setelah dikonversi, gabungkan semua angka kembali menjadi jawaban akhir.
(0+2+0) (4+2+0) = 2,6 = 26
26 = \(26_8\)