Garis adalah kurva lurus yang tidak berpangkal dan tidak berujung. Sudut dibentuk oleh dua sinar garis yang bersekutu titik pangkalnya. Sinar garis adalah kura lurus yang berpangkat tetapi tidak berujung sedangkan titik pangkal disebut titik sudut.
Garis dan sudut adalah materi yang menjadi kunci untuk mempelajari materi geometri. Dengan memahami konsep garis dan sudut, Gengs bisa dengan mudah mempelajari konsep bidang, bangun datar dan materi geometri lainnya.
Tanpa penjelasan panjang lebar lagi, berikut ini 10 soal garis dan sudut beserta penyelesaian.
Soal 1
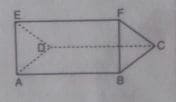
Rusuk-rusuk yang sejajar dengan CD adalah…
a. AB dan BC
b. AD dan BC
c. CF dan DE
d. AB dan EF
Jawaban: d
Soal 2
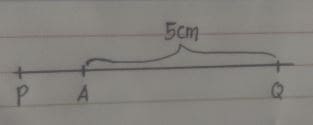
Perbandingan PA:PQ = 1:4. Titik A di tengah PQ. Jika panjang AQ=5 cm maka panjang PA= …. cm
a. 1 1/3
b. 1 2/3
c. 2 2/3
d. 3
Jawaban: b
Penyelesaian:
Kita buat garis seperti berikut ini.
PA/PQ = (Panjang PA)/(Panjang PQ)
1/4 = (Panjang PA)/(Panjang PA + Panjang AQ)
1/4 = (Panjang PA)/(Panjang PA + 5)
Panjang PA + 5 = 4 × Panjang PA
Panjang PA – 4 Panjang PA = -5
-3 Panjang PA = -5
Panjang PA = (-5)⁄(-3) = 5/3 =1 2/3
Soal 3
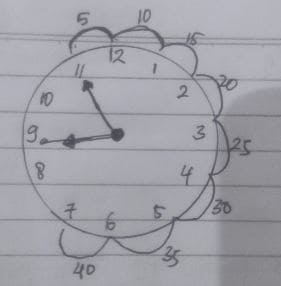
Mula-mula jam menunjukkan pukul 08.55. Setelah bergerak selama 40 menit, jarum panjang berputar … putaran.
a. 2/5
b. 2/3
c. ¾
d. 5/6
Jawabana: b
Penyelesaian:
Perhatikan gambar berikut.
Saat jarum panjang bergerak 5 menit maka jarum panjang telah berputar 1/12 putaran.
Karena jarum jam bergerak 40 menit maka jarum panjang berputar 8/12 putaran atau 2/3 putaran.
Soal 4
Besar sudut x pada gambar di atas adalah…
a. 20°
b. 30°
c. 40°
d. 50°
Jawaban: a
Penyelesaian:
70° + x = 90° (sudut saling berpenyiku)
x = 20°
Jadi, besar sudut x pada gambar di atas adalah 20°.
Soal 5
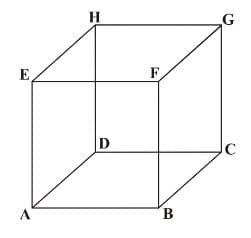
Pada gambar di atas, salah satu contoh garis vertikal dan horizontal masing-masing adalah…
a. AD dan BF
b. AB dan DC
c. AD dan BC
d. DH dan DC
Jawaban: d
Penyelesaian:
Garis-garis horizontal yaitu AB, BC, CD, AD, EF, FG, GH, dan EH.
Garis-garis ertikal yaitu AE, BF, CG, dan DH.
a. AD = garis horizontal dan BF = garis vertikal
b. AB = garis horizontal dan DC = garis horizontal
c. AD = garis horizontal dan BC = garis horizontal
d. DH = garis vertikal dan DC = garis horizontal
Karena pada soal yang ditanyakan yaitu garis vertikal dan horizontal maka yang tepat benar yaitu DH dan DC.
Soal 6
Perhatikan gambar berikut.
Besar pelurus sudut PQS adalah…
a. 105°
b. 96°
c. 84°
d. 75°
Jawaban: d
Penyelesaian:
∠PQS + ∠SQR = 180° (sudut berpelurus)
(5x)° + (3x + 12)° = 180°
5x° + 3x° + 12° = 180°
8x° = 180° – 12°
8x° = 168°
x° = 21°
Pelurus ∠PQS adalah ∠SQR.
∠SQR = (3x + 12)°
= (3 x 21 + 12)°
= (63 +12)°
= 75°
Jadi, besar pelurus ∠SQR adalah 75°.
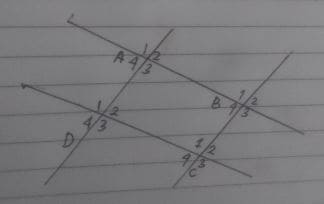
Soal 7
Perhatikan gambar berikut
Jika sudut A₂ = 45°, hasil dari ∠D₂ + ∠C₁ + ∠B₄ =….
a. 180°
b. 225°
c. 270°
d. 360°
Jawaban: b
Penyelesaian:
Mencari ∠D₂
∠A₂ = ∠B₂ = ∠C₂ = ∠D₂ = 45° (sudut sehadap)
Dari sini telah kita peroleh bahwa ∠D₂ = 45°.
Mencari ∠C₁
∠C₁ + ∠D₂ = 180° ( sudut dalam sepihak)
∠C₁ + 45° = 180°
∠C₁ = 180° – 45° = 135°
Dengan demikian, ∠C₁ = 135°
Mencari ∠B₄
∠B₄ = ∠A₂ = 45° (sudut dalam bersebrangan)
Dengan demikian, ∠B₄ = 45°
Karena kita telah peroleh ∠D₂, ∠C₁ dan ∠B₄ maka hasil dari ∠D₂ + ∠C₁ + ∠B₄ = 45° + 135° + 45° = 225°.
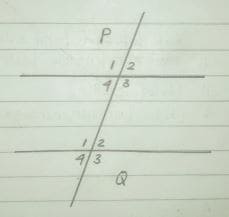
Soal 8
Perhatikan gambar di atas.
Jika besar <P₁=122°, besar <Q₄ adalah…
a. 32°
b. 46°
c. 58°
d. 61°
Jawaban: c
Penyelesaian:
∠P₁ = ∠Q₁ = 122° (sudut sehadap)
∠Q₁ = ∠P₃ = 122° (sudut dalam bersebrangan)
∠P₃ + ∠Q₂ = 180° (sudut dalam sepihak)
122° + ∠Q₂ = 180°
∠Q₂ = 180° – 122° = 58°
∠Q₂ = ∠P₂ = 58° (sudut sehadap)
∠P₂ = ∠Q₄ = 58° (sudut luar bersebrangan)
Jadi, besar ∠Q₄ adalah 58°.
Soal 9
Sudut A dan sudut B merupakan dua sudut yang saling berpelurus. Jika besar ∠A=(5x+2)° dan besar ∠B=(2x-4)°, besar ∠A adalah…
a. 48°
b. 54°
c. 78°
d. 132°
Jawaban: d
Penyelesaian:
∠A + ∠B = 180° (sudut saling berpelurus)
(5x+2)° + (2x-4)° = 180°
5x + 2x + 2 – 4 = 180°
7x – 2 = 180°
7x = 182°
x = 26
Dengan demikian, besar ∠A adalah:
∠A = (5x + 2)° = (5*26 + 2)° = 132°
Soal 10
Jika besar ∠A₁=78°, maka besar ∠B₂ adalah…
a. 78°
b. 90°
c. 102°
d. 180°
Jawaban: c
Penyelesaian:
Diketahui ∠A₁ = 78°
∠A₁ = ∠B₁ = 78° ( sudut sehadap)
∠A₁ = ∠B₃ = 78° (sudut luar bersebrangan)
∠B₃ = ∠A₃ = 78° (sudut sehadap)
∠A₃ + ∠B₂ = 180° (sudut dalam sepihak)
78° + ∠B₂ = 180°
∠B₂ = 180° – 78° = 102°
Dengan demikian, besar ∠B₂ adalah 102°.
Jangan lupa pelajari soal garis dan sudut lebih banyak lagi.