Sebelum latihan, ada baiknya jika kita pelajari materinya. Untuk pelajari materinya bisa klik Matriks – Penjumlahan/Pengurangan Dan Perkalian Dengan Skalar
Penjumlahan Matriks
Contoh 1
Misalkan diberikan matriks A berordo 2×2 dan B berordo 2×2 sebagai berikut:
Tentukan penjumlahan dari matriks A dan matriks B
Jawab:
Contoh 2
Misalkan diberikan matriks sebagai berikut:
Tentukan: S+T
Jawab:
Contoh 3
Diberikan matrik berordo 3×3, misalkan matriks P dan matriks Q sebagai berikut:
Tentukan penjumlahan dari matriks P dan matriks Q
Jawab:
Contoh 4
Misalkan diberikan matriks sebagai berikut:
Tentukan penjumlahan dari matriks A dan matriks B atau ( A + B )
Jawab:
Pengurangan Matriks
Contoh 1
Diberikan matrik berordo 2×2, misalkan matriks P dan matriks Q sebagai berikut:
$mathbf{P}=begin{bmatrix}2 & 3\ 6&9 end{bmatrix},mathbf{Q}=begin{bmatrix}3 & 1\ 7&5 end{bmatrix}$
Tentukan: P – Q
Jawab:
Contoh 2:
Misalkan diberikan matriks A berordo 3×3 dan B berordo 3×3 sebagai berikut:
Tentukan: A – B
Jawab:
Contoh 3
Misalkan diberikan matriks J dan Matriks K sebagai berikut:
$mathbf{J}=begin{bmatrix} 1 &2 &3 \ 6& 5& 4 end{bmatrix}, mathbf{K}=begin{bmatrix} 2 &4 &6 \ 1& 3 & 8 end{bmatrix}$
Tentukan: J – K
Jawab:
Contoh 4
Misalkan diberikan matriks sebagai berikut:
Tentukan: S – T
Jawab:
Perkalian Matriks
Contoh 1
Diberikan matriks A berordo 2×2 dan B berordo 2×2 sebagai berikut:
$mathbf{A}=begin{bmatrix} 2 &5 \ 4& 7 end{bmatrix}, mathbf{B}=begin{bmatrix} 3 & 7\ 1&6 end{bmatrix}$
Tentukan:
a. A . B
b. B . A
c. 5A
d. 3B
Jawaban a
Jawaban b
Jawaban c
$5.mathbf{A}=5.begin{bmatrix} 2 &5 \ 4& 7 end{bmatrix}$
$5.mathbf{A}=begin{bmatrix} 10&25\ 20& 35 end{bmatrix}$
Jawaban d
$3.mathbf{B}=3.begin{bmatrix} 3 & 7\ 1&6 end{bmatrix}$$3.mathbf{B}=begin{bmatrix} 9 & 21\ 3&18 end{bmatrix}$
Contoh 2
Tentukan hasil kali dari matriks A dan B jika matriksnya sebagai berikut:
$mathbf{A}=begin{bmatrix} 1\ 2\ 3 end{bmatrix}, mathbf{B}=begin{bmatrix} 3 &5 &2 end{bmatrix}$
Jawab:
Contoh 3
Tentukan hasil kali dari matriks A dan B jika matriksnya sebagai berikut:$mathbf{A}=begin{bmatrix} 3 &5 &2 end{bmatrix}, mathbf{B}=begin{bmatrix} 3\ 8\ 1 end{bmatrix}$
Jawab:
Contoh 4
Jika di berikan matriks P dan matriks Q seperti di bawah ini, Tentukan P . Q
Jawab:
Contoh 5:
Akan di buktikan IB = BI. Dimana I merupakan matriks identitas dan B adalah matriks berordo 3×3 seperti di bawah ini:
Jawab:
$mathbf{I}.mathbf{B}=mathbf{B}.mathbf{I}$
Terbukti
Penjumlahan, Pengurangan dan Perkalian Matriks
Contoh 1
Misalkan diberikan matriks A dan matriks B sebagai berikut:
$mathbf{A}=begin{bmatrix} 1 &3 \ 2 &4 end{bmatrix},mathbf{B}=begin{bmatrix} 4 &7 \ 5 &6 end{bmatrix}$
Tentukan:
a. 3A – B
b. A– 4B
c. 2A + B
Jawaban a
Jawaban b
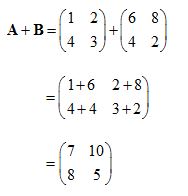
thanks ngebantu banget
Sama-sama. Terima kasih telah berkunjung. Semoga bermanfaat.
Perkalian bilangan real dan perkalian mayriks