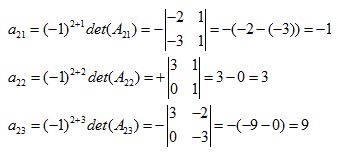Metode Sarrus hanya dapat digunakan untuk matriks 3×3. Perhitungan determinan suatu matriks dengan ukuran lebih besar sangat rumit jika menggunakan metode Sarrus. Salah satu cara menentukan determinan matriks segi adalah dengan minor-kofaktor elemen matriks tersebut.
Cara ini dijelaskan sebagai berikut:
Misalkan Aᵢⱼ adalah suatu matriks yang diperoleh dengan cara menghilangkan baris ke-i dan kolom ke-j dari suatu matriks Aₘₓₙ.
Didefinisikan sebagai berikut:
- Minor elemen aᵢⱼ diberi notasi Mᵢⱼ, adalah Mᵢⱼ=det(Aᵢⱼ).
- Kofaktor elemen aᵢⱼ, diberi notasi αᵢⱼ, adalah αᵢⱼ=(-1)ⁱ⁺ʲ.
Contoh:
Misalkan suatu matriks A berukuran 3×3 seperti berikut ini:
\(\begin{pmatrix} 1 &2 &3 \\ 4 &5 &6 \\ 7 &8 &9 \end{pmatrix}\)
maka diperoleh:
Definisi: Misalkan suatu matriks A = (aᵢⱼ)ₙₓₙ dan aᵢⱼ kofaktor elemen aᵢⱼ, maka:
Contoh 1:
Hitunglah determinan matriks berikut”
\(\begin{pmatrix} 3 &-2 &1 \\ 1 &3 &2 \\ 0 &-3 &1 \end{pmatrix}\)
Jawab:
Untuk menghitung determinan dari matriks tersebut kita gunakan definisi di atas, dengan memilih baris ke-2, sehingga:
det(A)=a₂₁ α₂₁+a₂₂ α₂₂+a₂₃ α₂₃
Dalam hal ini, a₂₁=1,a₂₂=3, a₂₃=2, dan
Dalam hal ini, a₂₁=1,a₂₂=3, a₂₃=2, dan
Selanjutnya dengan menggunakan definisi diatas lagi, kita juga bisa dengan memilih baris/kolom lainnya, misal dipilih kolom ke-3, maka:
\(\det(\mathbf{A})=a_{13}\alpha _{13}+a_{23}\alpha _{23}+a_{33}\alpha _{33}\)
dalam hal ini,\(a_{13}=1,a_{23}=2,a_{33}=1\), dan
dalam hal ini,\(a_{13}=1,a_{23}=2,a_{33}=1\), dan
Apabila kita perhatikan pada hasil akhir pada penyelesaiannya, kita akan dapatkan hasil yang sama. Maka kita cukup memilih satu baris atau kolom saja untuk mengerjakan soal seperti diatas.
Contoh 2:
Tentukan determinan matriks A₃ₓ₃ berikut ini:
\(\begin{pmatrix} a_{11} &a_{12} &a_{13} \\ a_{21} &a_{22} &a_{23} \\ a_{31} &a_{32} &a_{33} \end{pmatrix}\)
Jawab:
Dengan menggunakan definisi di atas, dengan memilih baris ke-1
Dengan menggunakan definisi di atas, dengan memilih baris ke-1
Perhatikan bahwa tanda untuk kofaktor bergantung pada penjumlahan i dan j. Untuk memudahkan perhitungan determinan dengan menggunakan minor-kofaktor, perhatikan tabel berikut:
Jika dipilih baris ke-1, maka: det(A)=a₁₁M₁₁-a₁₂M₁₂+…
Jika dipilih baris ke-2, maka: det(A)=a₂₁M₂₁-a₂₂M₂₂+…
dan seterusnya.
Demikian “Menentukan Determinan Matriks dengan Metode Minor Kofaktor“. Semoga bermanfaat.