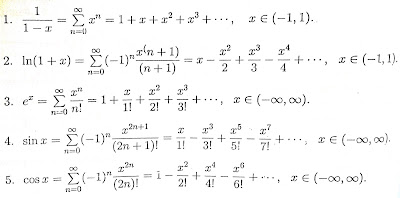Pada kesempatan kali ini kita akan menyelidiki masalah yang lebih umum yaitu fungsi manakah yang mempunyai penyajian deret pangkat dan bagaimana menentukannya?
Kita akan memulainya dengan memisalkan suatu fungsi f sebagai sembarang fungsi yang dapat kita nyatakan sebagai deret pangkat.
f(x)=c₀ + c₁(x-a) + c₂(x-a)² + c₃(x-a)₃ + …
Substitusikan x = a pada persamaan di atas sehingga akan menghasilkan f(a)=c₀.Jika persamaan f(x) di atas diturunkan, maka akan di peroleh sebagai berikut.
f'(x)=c₁ + 2c₂(x-a) + 3c₃(x-a)² + 4c₄(x-a)₃ + …
dimana |x – a| < R.
Substitusikan x = a pada persamaan di atas sehingga akan menghasilkan f'(a)=c₁.
Jika persamaan f ‘(x) di atas diturunkan, maka akan diperoleh hasil sebagai berikut ini.
f”(x)=2c₂ + 2.3c₃(x-a) + 3.4c₄(x-a)² +…
dimana |x – a| < R.
Substitusikan x = a pada persamaan di atas sehingga akan menghasilkan f”(a)=2c₂.
Jika persamaan f ”(x) diturunkan, maka kita akan peroleh persamaan f ”'(x) seperti berikut ini.
f”'(x)=2.3c₃ + 2.3.4c₄(x-a) + 3.4.5c₅(x-a)² + …
dimana| x-a| < R.
Substitusikan x = a pada persamaan f ”'(x) di atas sehingga akan menghasilkan f”'(a)=2.3c₃ = 3!c₃.
Jika proses di atas dilanjutkan terus, maka secara umum kita akan peroleh:
\(f^{n}(a)=2\times 3\times 4\times 3\times …\times n\times c_{n}\)
ATAU
\(c_{n}=\frac{f^{{n}}a}{n!}\)
Jika f mempunyai penyajian deret pangkat di a, yaitu jika
\(f(x)=\sum_{n=0}^{\infty }c_{n}(x-a)^{n},\mid x-a \mid < \mathbb{R}\)
maka koefisiennya diberikan oleh:
\(c_{n}=\frac{f^{n}a}{n!}\)
CATATAN
Koefisien cₙ di atas adalah tunggal. Jadi, jika f memiliki penyajian deret pangkat di a, maka deretnya pasti berbentuk:
\(f(x)=\sum_{n=0}^{\infty }\frac{f^{n}a}{n!}(x-a)^{n}\)
\(f(x)=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f”(a)}{2!}(x-a)^{2}+\frac{f”'(a)}{3!}(x-a)^{3}+…\)
Suatu fungsi tidak dapat digambarkan oleh lebih dari satu deret pangkat dari (x – a).
Deret pada persamaan di atas disebut deret Taylor dari fungsi f di a (atau di sekitar a atau yang berpusat di a).
Untuk kasus khusus saat a = 0, maka deret Taylor-nya akan menjadi seperti berikut ini:
\(f(x)=\sum_{n=0}^{\infty }\frac{f^{n}(0)}{n!}x^{n}=f(0)+\frac{f'(0)}{1!}x+\frac{f”(0)}{2!}x^{2}+\frac{f”'(0)}{3!}x^{3}+…\)
Deret ini sering muncul sehingga diberi nama khusu sebagai deret Maclaurin.
Teorema Taylor
Misalkan f adalah fungsi yang memiliki turunan pada semua tingkatan untuk \(x\in (a-\mathbb{R},a+\mathbb{R})\). Syarat perlu dan syarat cukup agar fungsi tersebut sama dengan deret Taylor-nya adalah
\(\lim_{n\rightarrow \infty }R_{n}(x)=0\)
dengan \(R_{n}(x)\) adalah suku sisa dalam rumus Taylor, yaitu:
\(R_{n}(x)=\frac{f^{n+1}(c)}{(n+1)!}(x-a)^{n+1}\)
untuk sembarang \(c\in (a-\mathbb{R},a+\mathbb{R})\)
CATATAN
1. Jika kita ingin mengetahui nilai fungsi f(x) untuk x di sekitar a, maka lebih baik menggunakan deret Taylor untuk fungsi tersebut di a.
2. Jika \(\lim_{n\rightarrow \infty }R_{n}(x)\neq 0\), maka deret Taylor untuk fungsi f(x) mungkin saja konvergen pada suatu selang, tetapi tidak menggambarkan fungsi f(x) pada selang tersebut.
Misalkan \(f(x)=\sum_{n=0}^{\infty }a_{n}x^{n}\) dan \(g(x)=\sum_{n=0}^{\infty }b_{n}x^{n}\) adalah dua deret pangkat yang masing-masing konvergen untuk paling tidak \(\mid x \mid < \mathbb{R}\), dengan R suatu bilangan nyata. Jika penjumlahan, pengurangan, perkalian dan pembagian dilakukan terhadap deret-deret tersebut dengan memperlakukannya sebagai suku banyak, maka deret-deret yang diperoleh akan konvergen untuk \(\mid x \mid < \mathbb{R}\), dan masing-masing menyatakan fungsi \(f(x)+g(x),f(x)-g(x),f(x)g(x) dan f(x)/g(x)\) jika \(g_{0}\neq 0\).
Deret Binomial merupakan salah satu bentuk khusus dari deret Maclaurin.
Teorem deret Binomial
Untuk setiap bilangan nyata p dan x dengan |x| < 1 berlaku
\((1+x)^p =1+\begin{pmatrix} p\ 1 \end{pmatrix}x+\begin{pmatrix} p\ 2 \end{pmatrix}x^2 +\begin{pmatrix} p\ 3 \end{pmatrix}x^3+…\)
dengan
\(\begin{pmatrix} p\ k \end{pmatrix}=\frac{p(p-1)(p-2)…(p-k+1)}{k!}\)
Beberapa deret Maclaurin yang penting
Demikian Rangkuman Materi – Deret Taylor, Maclaurin Dan Deret Binomial.
Semoga bermanfaat.