Pada kesempatan kali ini, saya akan berbagi 20 contoh soal matematika kelas 12 beserta penyelesaiannya.
Soal 1
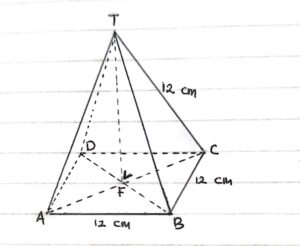
Diketahui limas segi empat beraturan T. ABCD dengan panjang AB=12 cm dan TA=12 cm. Titik E merupakan titik perpotongan diagonal alas ABCD. Jika titik F merupakan titik tengah antara titik E dan C, jarak titik T ke F adalah…
Jawab:
Pertama-tama kita gambarkan sebuah limas T.ABCD seperti berikut.
Menentukan panjang CS dengan menggunakan kesamaan luas segitiga.
1/2 ⨯ PQ ⨯ CS = 1/2 ⨯ QC ⨯ CP
PQ ⨯ CS = QC ⨯ CP
5√3 ⨯ CS = 5√2 ⨯ 5
√3 ⨯ CS = 5√2
CS = 5√2 / √3
= (5√6) / 3
Jadi, jarak antara titik C ke bidang BPD adalah 5√6 /3 cm.
Soal 3
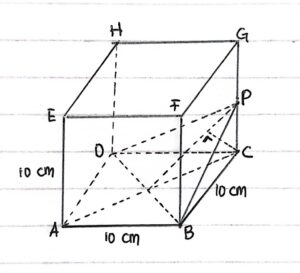
Diketahui balok ABCD.EFGH dengan ukuran seperti gambar berikut.
Jarak titik H ke garis AG sama dengan panjang HP.
Segitiga AGH siku-siku di H.
AH merupakan diagonal bidang ADHE.
AH² = AD² + DH²
= 6² + 8²
= 36 + 64
= 100
AH = √(100 ) = 10 cm
AG merupakan diagonal ruang balok.
AG² = AH² + HG²
= 10² + 24²
= 100 + 576
= 676
AG = √(676) = 26 cm
Luas segitiga AGH dapat dihitung menggunakan rumus 1/2 ⨯ AH ⨯ HG atau 1/2 ⨯ AG ⨯ HP sehingga diperoleh:
1/2 ⨯ AH ⨯ HG = 1/2 ⨯ AG ⨯ HP
1/2 ⨯ 10 ⨯ 24 = 1/2 ⨯ 26 ⨯ HP
120 = 13 ⨯ HP
HP = 120/13
Jadi, jarak titik H ke garis AG adalah 120/13 cm.
Soal 4
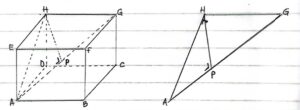
Diketahui limas beraturan T.ABCD dengan panjang rusuk 6 cm. Jika P titik tengah CD, jarak titik P ke bidang TAB adalah…
Jawab:
Limas T. ABCD dapat digambarkan sebagai berikut:
Pada segitiga PQR berlaku PR²=PQ²-QR² dan pada segitiga PRT berlaku PR²=PT²-TR²; sehingga;
PQ²-QR²=PT²-TR²
6²-x²=(3√3)²-(3√3 – x)²
36-x²=27-(27-6√3 x + x²)
36-x²=27-27+6√3 x -x²
36-x²=6√3 x -x²
6√3 x = 36
x = 36/6√3 = 2√3
Diperoleh panjang QR = 2√3 cm
PR²=PQ²-QR²
=6²-(2√3)²
=36-12
=24
PR = √(24) = 2√6
Jadi, jarak titik P ke bidang TAB adalah 2√6 cm.
Soal 5
Dina akan menyusun 7 buah buku berjajar di rak buku. Tiga diantara 7 buku tersebut merupakan buku berseri yang harus diletakan berdampingan. Banyak susunan buku di rak yang mungkin adalah…
Jawab:
Mencari banyak susunan buku merupakan permasalahan permutasi.
Tiga buku yang berseri harus disusun berdampingan sehingga dihitung sebagai satu kelompok di antara 7 – 3 = 4 buku lainnya. Banyak susunan 4 buku tidak berseri dan satu kelompok buku berseri adalah ₅P₅ cara.
Kelompok buku berseri terdiri atas 3 buku sehingga banyak susunan yang mungkin ada ₃P₃ cara.
Banyak kemungkinan susunan buku
= ₅P₅ ⨯ ₃P₃
= 5! ⨯ 3!
= (5⨯4⨯3⨯2⨯1) x (3⨯2⨯1)
= 120 ⨯ 6
= 720
Jadi, banyak kemungkinan susunan buku adalah 720 cara.
Soal 6
Sekelompok siswa terdiri atas 6 siswa laki-laki dan 9 siswa perempuan. Dari kelompok dipilih 5 orang terdiri atas 2 laki-laki dan 3 perempuan untuk mengikuti suatu kegiatan. banyak pemilihan yang mungkin adalah…
Jawab:
Pemilihan siswa tidak memperlihatkan urutan, maka pemilihan siswa merupakan permasalahan kombinasi.
Banyak cara memilih 2 dari 6 siswa laki-laki adalah ₆C₂.
Banyak cara memilih 3 dari 9 siswa perempuan adalah ₉C₃.
Banyak hasil pemilihan
= ₆C₂ ⨯ ₉C₃
= (6! /(2! ⨯ (6-2)! )) ⨯ (9! / (3! ⨯ (9-3)! ))
= (6! / 2! 4!) ⨯ (9! / 3! 6!)
= (6⨯5⨯4! / 2⨯1⨯4!) x (9⨯8⨯7⨯6! / 3⨯2⨯1⨯6!)
= (30/2) x (504/6)
= 15 ⨯ 84
= 1.260
Jadi, banyak hasil pemilihan yang mungkin adalah 1.260.
Soal 7
Sebuah dadu dilambungkan sekali, jika A adalah kejadian muncul bilangan ganjil dan B adalah kejadian muncul bilangan genap. Tentukan peluang kejadian munculnya bilangan ganjil dan genap!
Jawab:
S = {1,2,3,4,5,6}
n(S) = 6
A = bilangan ganjil = {1,3,4}
n(A)=3
B = bilangan genap = {2,4,6}
n(B)=3
P(A) = 3/6 = 1/2
P(B) = 3/6 = 1/2
A ∩ B = { }
n(A ∩ B) = 0 (kejadian saling lepas)
P(A ∪ B) = P(A) + P(B) = 1/2 + 1/2 = 1
Soal 8
Sebuah dadu dilambungkan sekali, jika A kejadian munculnya bilangan ganjil dan B adalah kejadian munculnya bilangan prima. Tentukan peluang munculnya bilangan ganjil atau prima!
Jawab:
S = {1,2,3,4,5,6}
n(S) = 6
Diketahui:
A = Muncul bilangan ganjil
B = Muncul bilangan prima
A = {1,3,5}
n(A) = 3
B={2,3,5}
n(B) = 3
P(A) = n(A) /n(S) = 3/6 = 1/2
P(B) = n(B) /n(S) = 3/6 = 1/2
A ∩ B = {3,5}
n(A∩B)=2
P(A ∩ B) = n(A∩B)/n(S) = 2/6 = 1/3
P(A ∪ B) = P(A) + P (B) – P(A∩B)
= 1/2 + 1/2 – 1/3
= 2/3
Soal 9
Tiara dan Nabila mengikuti sebuah kejuaraan bulu tangkis. Mereka bertemu lawan yang berbeda. Peluang Tiara lolos ke babak berikutnya 65%, sedangkan Nabila lolos ke babak berikutnya 40%. Peluang salah satu dari keduanya lolos ke babak berikutnya adalah…
Jawab:
Misalkan:
A = kejadian Tiara lolos ke babak berikutnya
B = kejadian Nabila lolos ke babak berikutnya
maka:
P(A) = 65% = 0,65
P(B) = 40% = 0,4
P(Aᶜ) = 1 – 0,65 = 0,35
P(Bᶜ) = 1 – 0,4 = 0,6
Hasil kejadian A tidak mempengaruhi hasil kejadian B maka kejadian A dan B saling bebas.
Peluang A terjadi dan B tidak terjadi:
P(A ∩ Bᶜ) = P(A) ⨯ P(Bᶜ) = 0,65 ⨯ 0,6 = 0,39
Peluang A tidak terjadi dan B terjadi:
P(Aᶜ ∩ B) = P(Aᶜ) ⨯ P(B) = 0,35 ⨯ 0,4 = 0,14
Peluang salah satu dari kejadian A dan B terjadi:
P = P (A ∩ Bᶜ) + P(Aᶜ ∩ B) = 0,39 + 0,14 = 0,53
Jadi, peluang salah satu lolos ke babak berikutnya adalah 0,53.
Soal 10
Suatu mesin permainan melempar bola bernomor 1,2,3,4,5,6,7,8,9,10 sebanyak 70 kali. Frekuensi harapan muncul bola dengan nomor bilangan prima adalah…
Jawab:
Ruang sampelnya yaitu:
S = {1,2,3,4,5,6,7,8,9,10}
n(S) = 10
Misalkan:
A = kejadian muncul bola dengan nomor bilangan prima
A = {2,3,5,7}
n(A) = 4
Mencari peluang terjadi A
P(A) = n(A) / n(S) = 4/10 = 2/5
Frekuensi harapan A dari 70 percobaan yaitu:
Fh = P(A) ⨯ N = 2/5 ⨯ 70 = 28
Jadi, frekuensi harapan diperoleh hasil nomor bilangan prima adalah 28 kali.
Soal 11
Sebuah tim terdiri atas seorang ketua, seorang sekertaris dan enam orang anggota. Mereka akan berunding pada sebuah meja bundar. Jika ketua dan sekertaris harus duduk berdampingan, banyak susunan duduk yang mungkin adalah …
Jawab:
Mencari banyak susunan duduk mengelilingi meja bundar merupakan permasalahan permutasi siklik.
Ketua dan sekertaris harus duduk berdampingan, maka:
Banyak kemungkinan duduk melingkar = (7-1)! = 6!
Banyak kemungkinan duduk ketua dan sekertaris = ₂P₂ = 2!
Seluruh kemungkinan susunan duduk
= 6! x 2!
= (6⨯5⨯4⨯3⨯2⨯1) x (2⨯1)
= 720 ⨯ 2
= 1,440
Jadi, banyak susunan duduk yang mungkin adalah 1.440 cara.
Soal 12
Banyak bilangan ratusan ganjil yang dapat disusun dari angka-angka 0,1,2,3,4 dan 5 adalah…
Jawab:
Bilangan ratusan terdiri atas 3 digit. Digit pertama ratusan, digit kedua puluhan dan digit ketiga satuan.
Bilangan ratusan ganjil, digit satuannya ganjil.
Perhatikan penjabaran singkat berikut.
Ratusan Digit ratusan dapat dipilih dari angka 1,2,3,4 dan 5.
Puluhan Digit puluhan dapat dipilih dari angka 0,1,2,3,4 dan 5.
Satuan Digit satuan dapat dipilih dari angka 1,3 dan 5.
Dari penjabaran singkat di atas diperoleh:
Banyak pilihan angka pada digit ratusan ada 5.
Banyak pilihan angka pada digit puluhan ada 6.
Banyak pilihan angka pada digit satuan ada 3.
Banyak bilangan yang dapat disusun:
n = 5⨯6⨯3=90
Jadi, banyak bilangan yang dapat disusun adalah 90.
Soal 13
Pak Aris mempunyai 10 lampu LED dan 4 lampu diantaranya mati. Pak Aris akan memasang lampu tersebut pada dua tempat. Pak Aris mengambil satu lampu dan memasangnya pada tempat lampu pertama, lalu mengambil lagi satu lampu dan memasangnya pada tempat kedua. Peluang diperoleh 2 lampu hidup pada pemasangan pertama dan kedua adalah…
Jawab:
Diketahui: Dari 10 lampu LED terdiri atas 4 lampu mati dan 6 lampu hidup, diambil satu per satu tanpa pengembalian.
Misalkan:
A = Kejadian diperoleh lampu hidup pada pemasangan pertama
= Kejadian diperoleh 1 dari 6 lampu hidup pada pemasangan pertama
S₁ = Kejadian terambil 1 dari 10 lampu LED
P(A) = 6/10
B = Kejadian diperoleh lampu hidup pada pemasangan kedua
= kejadian diperoleh 1 dari 5 lampu hidup yang tersisa pada pemasangan kedua
S₂ = Kejadian terambil 1 dari 9 lampu Led yang tersisa
Peluang B terjadi dengan syarat A telah terjadi:
P(B|A) 5/9
Peluang diperoleh lampu hidup pada pemasangan pertama dan kedua:
P(A ∩ B) = P(A) ⨯ P(B|A)
= 6/10 ⨯ 5/9
= 30/90
= 1/3
Jadi, peluang diperoleh lampu hidup pada pemasangan pertama dan kedua adalah 1/3.
Soal 14
Hasil pengukuran tinggi badan siswa kelas XII disajikan dalam ogive berikut.
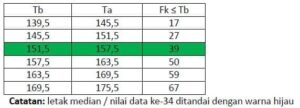
Median terletak pada kelas interval yang memiliki Tb = 151,5 dan Ta = 157,5 sehingga didapatkan:
L₂ = 151,5 (tepi bawa kelas median)
∑f₂ = 27 (jumlah frekuensi sebelum kelas median)
f₂ = 39 – 27 = 12 (frekuensi kelas median)
p = 157,5 – 151,5 = 6 (panjang kelas interval)
Dengan demikian,
Me = L₂ + [(n/2 – ∑f₂)/f₂] ⨯ p
= 151,5 + [(67/2 – 27)/12] ⨯ 6
= 151.5 + [ (33,5 – 27)/2 ]
= 151,5 + (6,5/2)
= 151,5 + 3,25
= 154,75
Jadi, median tinggi badan siswa adalah 154,75 cm.
Soal 15
Hasil pengukuran tinggi badan 30 siswa disajikan dalam histogram berikut:

Dengan demikian, rata-rata tinggi badan yaitu:
x = 4590 / 30 = 153
Jadi, rata-rata tinggi badan siswa adalah 153 cm.
Soal 16
Perhatikan tabel berikut yang menyatakan hasil penilaian guru terhadap hasil belajar matematika.
Dari tabel terlihat Q₃ terletak pada kelas interval 70-79 sehingga diperoleh:
L₃ = 70 (tepi bawa kelas kuartil atas)
∑f_Q₃ = 27 (jumlah frekuensi sebelum kelas kuartil atas)
f_Q₃ = 10 (frekuensi kelas kuartil atas)
p = 79-70+1 = 10 (panjang kelas interval)
Dengan demikian,
Q₃ = L₃ + [(3n/4 – ∑f_Q₃)/f_Q₃] ⨯ p
= 70 + [(3/4(40) – 27)/10] ⨯ 10
= 70 + [ (30 – 27)/10 ]
= 70 + 3
= 73
Jadi, kuartil atas hasil penilaian guru terhadap hasil belajar matematika adalah 73.
Soal 17
Simpangan baku data 4,2,6,12,2,8,4,10 adalah…
Jawab:
Jumlah data (n) = 8
x = (4+2+6+12+2+8+4+10)/8 = 48/8 = 6
∑(xᵢ – x) =(4-6)²+(2-6)²+(6-6)²+(12-6)²+(2-6)²+(8-6)²+(4-6)²+(10-6)²
= (-2)²+(-4)²+(0)²+(6)²+(-4)²+(2)²+(-2)²+(4)²
= 4+16+0+36+16+4+4+16
=96
Simpangan baku:
S² = (1/n) ∑(xᵢ – x)
= 1/8 (96)
= 12
S = √(12 ) = 2√3
Jadi simpangan baku data tersebut adalah 2√3.
Soal 18
Diketahui data 2,6,7,1,4. Nilai ragam data tersebut adalah…
Jawab:
Jumlah data (n) = 5
Pertama-tama kita cari rata-ratanya:
x= (2+6+7+1+4)/5 = 20/5 = 4
Selanjutnya, kita akan cari ragam data:
V = S²
S² = (1/n) ∑(xᵢ – x)²
= (1/5) ((2-4)²+(6-4)²+(7-4)²+(1-4)²+(4-4)²)
= (1/5) ((-2)²+(2)²+(3)²+(-3)²+(0)²)
= (1/5) (4+4+9+9+0)
= (1/5) (26) = 26/5
Soal 19
Simpangan rata-rata dari data 8,6,8,7,8,5 adalah…
Jawab:
Langkah awal, cari rata-rata:
x = (8+6+8+7+8+5)/6 = 42/6 = 7
Selanjutnya mencari simpangan rata-rata:
SR = (1/n) ∑|xᵢ – x|
= (1/6) (|8-7|+|6-7|+|8-7|+|7-7|+|8-7|+|5-7|)
= (1/6) (1+1+1+0+1+2)
= (1/6) (6) = 1
Jadi simpangan rata-rata data tersebut adalah 1.
Soal 20
Tabel berikut merupakan data waktu yang diperlukan 50 siswa dalam melakukan percobaan.