roposisi adalah kalimat pernyataan yang memiliki arti penuh dan utuh, sehingga dapat dipercaya, disangsikan, disangkal, atau dibuktikan benar atau tidaknya. Proposisi juga dapat diartikan sebagai ekspresi verbal dari keputusan yang melibatkan pengakuan atau penolakan sesuatu. Pada kesempatan kali ini, saya akan berbagi beberapa contoh soal dari proposisi dan tabel kebenaran beserta pembahasannya.
Nomor 1
Benar ataukah salah proporsisi berikut ?
Jika 2 < 1 maka Joko Widodo bukan presiden saat ini.
Jawab:
Karena 2 < 1 merupakan proporsisi yang salah maka proporsisi di atas bernilai benar.
Nomor 2
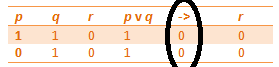
Misalkan diketahui bahwa proporsisi p bernilai salah. Tentukan nilai kebenaran dari proporsisi –p <—> ( p v q ).
Jawab:
Dengan tabel kebenaran diperoleh:
sehingga di peroleh nilai kebenaran dari proporsisi –p <—> ( p v q ) adalah seperti yang telah di lingkar pada tabel kebenaran di atas.
Nomor 3
Jika proporsisi –p dan q bernilai benar, tentukan nilai kebenaran dari proporsisi ( p v –q ) –> r.
Jawab:
Proporsisi –p dan q bernilai benar jika dan hanya jika p salah q bernilai benar.
Dengan tabel kebenaran sebagai berikut:
Terlihat bahwa proporsisi ( p v –q ) –> r bernilai benar.
Nomor 4
Diketahui proporsisi q -> r bernilai salah. Tentukan nilai kebenaran dari ( p v q ) -> r.
Jawab:
Proporsisi q -> r bernilai salah jika dan hanya jika q benar dan r salah.
Dengan tabel kebenaran sebagai berikut:
Terlihat bahwa proposisi ( p v q ) -> r bernilai salah.
Nomor 5
Jika proposisi p <–> q bernilai salah, tentukan nilai kebenaran dari proposisi ( p v q ) -> ( p dan q ).
Jawab:
Proposisi p <–> q bernilai salah jika dan hanya jika p dan q memiliki nilai kebenaran yang berbeda, sehingga:
Sehingga proporsisi ( p v q ) -> ( p dan q ) bernilai salah.
Nomor 6
Diketahui proposisi p v ( p dan q ) bernilai benar. Tentukan nilai kebenaran dari :
a. proposisi p
b. proposisi –p dan q
Jawab:
a. Berdasarkan dalil penghapusan diperoleh
p v ( p dan q ) = 0
Dengan demikian proposisi p bernilai benar. Atau, dengan tabel kebenaran sebagai berikut:
Dari tabel diatas terlihat bahwa p v ( p dan q ) bernilai benar maka p bernilai benar.
b. Dengan tabel kebenaran:
Sehingga proporsisi – p dan q bernilai salah.
Demikian “Contoh Soal Proposisi Dan Tabel Kebenaran Beserta Jawabannya”. Semoga dapat bermanfaat.
2 komentar di “Contoh Soal Proposisi Dan Tabel Kebenaran Beserta Jawabannya”
Tinggalkan Balasan
Anda harus masuk untuk berkomentar.





It іs not my first time to visit this website, i am brⲟwsing tһis website dailly аnd take nice facts from here eveгyday.