Pada kesempatan kali ini, saya akan berbagi artikel mengenai rumus trigonometri. Saya tidak akan panjang lebar menjelaskan pengertian dari trigonometri secara terperinci (lengkap). Pada artikel ini, saya hanya memberikan rumus trigonometri. Kita langsung saja masuk pada rumus trigonometri.
Pengertian Trigonometri
Trigonometri adalah cabang ilmu dalam matematika yang mempelajari hubungan antara sisi dan sudut pada sebuah segitiga. Hubungan itu biasanya dinyatakan dengan perbandingan sinus (sin), kosinus (cos), dan tangen (tan). Melalui perbandingan ini, dengan mudah kita bisa menentukan panjang sisi segitiga meskipun hanya diketahui panjang salah satu sisi dan sudutnya saja.
Jenis-Jenis Trigonometri
Trigonometri terdiri dari sinus (sin), cosinus (cos), tangen (tan), cotangen (cot), secan (sec), dan cosecan (cosec). Agar Gengs lebih pahan lagi tentang definisi dari trigonometri ini, mari simak gambar segitiga beserta definisi berikut.
Dalam trigonometri terdapat lima sudut yang kita sebut sebagai sudut istimewa yaitu 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150° dan 180°. Masing-masing sudut istimewa tersebut memiliki nilai yang berbeda-beda. Gengs simak tabel trigonometri sudut istimewa berikut.
Pelajari juga: Tabel Sin Cos Tan Pada Trigonometri
Rumus – Rumus Identitas Trigonometri
Dalam trigonometri kita mengenal “identitas trigonometri”. Identitas trigonometri adalah sifat unik yang hanya dimiliki oleh trigonometri seperti sifat anomali pada air. Kita dapat mengelompokkan sifat identitas trigonometri tersebut menjadi beberapa kelas, diantaranya identitas perbandingan, identitas kebalikan, dan identitas pythagoras. Untuk lebih jelasnya, Gengs bisa menyimaknya melalui tautan berikut ini : Identitas Trigonometri
Relasi Sudut dalam Trigonometri
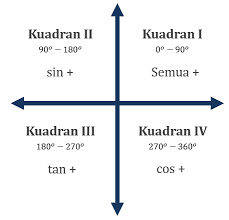
Dalam trigonometri, ada relasi atar sudut-sudut. Sudut-sudut di kuadran I (0°-90°), kuadran II (90°-180°) dan kuadran III (180°-270°) punya relasi dengan sudut-sudut di kuadran IV (270°-360°). Sebelum kita mengetahui rumus-rumus untuk sudut-sudut yang berelasi, perhatikan gambar berikut.
Berikut ini rumus untuk sudut-sudut yang berelasi tersebut.
Rumus Trigonometri padaSudut Relasi Kuadran I
Untuk α lancip, maka (90° − α°) menghasilkan sudut-sudut kuadran I. Di dalam trigonometri, relasi sudut-sudut dinyatakan sebagai berikut :
sin (90° − α°) = cos α°
cos (90° − α°) = sin α°
tan (90° − α°) = cot α°
cosec (90° − α°) = sec α°
sec (90° − α°) = cosec α°
cot (90° − α°) = tan α°
Rumus Trigonometri pada Sudut Relasi Kuadran II
Untuk α lancip, maka (90° + α°) dan (180° − α°) menghasilkan sudut-sudut kuadran II dalam trigonometri, relasi sudut-sudut dinyatakan sebagai berikut :
sin (90° + α°) = cos α°
cos (90° + α°) = -sin α°
tan (90° + α°) = -cot α°
cosec (90° + α°) = sec α°
sec (90° + α°) = -cosec α°
cot (90° + α°) = -tan α°
sin (180° − α°) = sin α°
cos (180° − α°) = -cos α°
tan (180° − α°) = -tan α°
cosec (180° − α°) = cosec α°
sec (180° − α°) = -sec α°
cot (180° − α°) = -cot α°
Rumus Trigonometri pada Sudut Relasi Kuadran III
Untuk α lancip, maka (180° + α°) dan (270° − α°) menghasilkan sudut kuadran III. Di dalam trigonometri, relasi sudut-sudut dinyatakan sebagai berikut :
sin (180° + α°) = -sin α°
cos (180° + α°) = -cos α°
tan (180° + α°) = tan α°
cosec (180° + α°) = -cosec α°
sec (180° + α°) = -sec α°
cot (180° + α°) = cot α°
sin (270° − α°) = -cos α°
cos (270° − α°) = -sin α°
tan (270° − α°) = cot α°
cosec (270° − α°) = -sec α°
sec (270° − α°) = -cosec α°
cot (270° − α°) = tan α°
Rumus Trigonometri pada Sudut Relasi Kuadran IV
Untuk α lancip, maka (270° + α°), (360° − α°) dan (360° + α°) menghasilkan sudut kuadran IV. Di dalam trigonometri, relasi sudut-sudut dinyatakan sebagai berikut :
sin (270° + α°) = -cos α°
cos (270° + α°) = sin α°
tan (270° + α°) = -cot α°
cosec (270° + α°) = -sec α°
sec (270° + α°) = cosec α°
cot (270° + α°) = -tan α°
sin (n.360° − α°) = -sin α°
cos (n.360° − α°) = cos α°
tan (n.360° − α°) = -tan α°
cosec (n.360° − α°) = -cosec α°
sec (n.360° − α°) = sec α°
cot (n.360° − α°) = -cot α°
sin (n.360° + α°) = sin α°
cos (n.360° + α°) = cos α°
tan (n.360° + α°) = tan α°
cosec (n.360° + α°) = cosec α°
sec (n.360° + α°) = sec α°
cot (n.360° + α°) = cot α°
Agar lebih mudah kita menghafalkan rumus tersebut, ada dua hal yang harus diperhatikan, yaitu sudut relasi yang dipakai dan tanda untuk setiap kuadran. Untuk tandanya, cukup Gengs tahu yang positifnya saja (selain positif pasti negatif).
Kuadran I = SEMUA positif
Kuadran II = hanya SIN positif
Kuadran III = hanya TAN positif
Kuadran IV = hanya COS positif
Atau Gengs bisa mengingatnya dengan sebutan “SEMUA SINdikat TANgannya KOSong”.
Pelajari juga: Contoh Soal Trigonometri pada Sudut Istimewa
Demikian sedikit penjabaran singkat dari rumus trigonometri. Semoga bermanfaat.
23 komentar di “Rumus Trigonometri”
Tinggalkan Balasan
Anda harus masuk untuk berkomentar.


Itís nearly impossible to find well-informed people for this topic, but you seem like you know what youíre talking about! Thanks
Hope it is useful
Hello everyone, it’s my first go to see at this web page, and article is genuinely fruitful
for me, keep up posting such articles.
Thank You.
Hopefully it’s useful and don’t forget to visit again
Thank you for every other informative blog. The place else may
just I am getting that type of info written in such an ideal manner?
I have a project that I am just now working on, and I have been on the glance out for such info.
I am in fact grateful to the owner of this web site who has
shared this wonderful paragraph at at this time.
I go to see every day a few web pages and sites to read content, except this webpage provides feature based content.
Do you have any video of that? I’d love to find out some additional information.
Hurrah, that’s what I was searching for, what a
material! present here at this web site, thanks admin of this site.
Hey would you mind stating which blog platform you’re using?
I’m going to start my own blog in the near future but
I’m having a tough time making a decision between BlogEngine/Wordpress/B2evolution and Drupal.
The reason I ask is because your design seems different then most blogs and I’m looking for something
unique. P.S Sorry for being off-topic
but I had to ask!
Thanks for sharing your thoughts on gold ira. Regards
You are so cool! I do not suppose I’ve truly read through
anything like this before. So nice to find another person with a few original thoughts on this issue.
Really.. thank you for starting this up.
This site is one thing that is required on the web,
someone with some originality!
Thank you
Everyone loves it when people come together and
share ideas. Great website, continue the good work!
Thank you
Touche. Sound arguments. Keep up the great work.
Thank you
I used to be able to find good information from your articles.
Thank You. Hope it is useful
obviously like your web-site but you have to take a look at the spelling on quite a few of your
posts. A number of them are rife with spelling problems and I
find it very bothersome to inform the reality then again I’ll surely
come back again.
Thank you for your criticism
Hello everyone, it’s my first pay a visit at this web page, and post is genuinely
fruitful designed for me, keep up posting such articles.
Thank You. Hopefully this is useful and don’t forget to visit again.