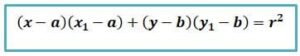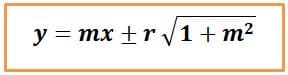Persamaan Lingkaran – Pada kesempatan kali ini kita akan belajar tentang rumus matematika SMA kelas 11 tentang persamaan lingkaran. Kita akan mengetahui rumus dari persamaan lingkaran diantaranya kedudukan titik terhadap lingkaran, kedudukan garis terhadap lingkaran dan persamaan garis singgung lingkaran. Lingkaran adalah tempat kedudukan titik-titik pada suatu bidang yang berjarak sama terhadap suatu titik tertentu.
Berikut ini rumus-rumus yang dipakai dalam materi tentang persamaan lingkaran yang dipelajari pada jenjang SMA.
PERSAMAAN LINGKARAN
1. Persamaan lingkaran yang berpusat di P(0,0) dan memiliki jari-jaru (r) adalah: x²+y²=r²
2. Persamaan lingkaran yang berpusat di P(a,b) dan memiliki jari-jari (r) adalah: (x-a)²+(y-b)²=r²
3. Bentuk umum persamaan lingkaran: x²+y²+2Ax+2By+C=0
Titik pusat lingkaran: P(-A,-B)
Jari-jari lingkaran: r² = A²+B²-C
dengan:
A,B dan C adalah bilangan real
A²+B²≥C
KEDUDUKAN TITIK TERHADAP LINGKARAN
1. Untuk titik pusat lingkaran P(0,0)
a. Suatu titik A(x,y) terletak di dalam lingkaran yang berpusat di P(0,0) dan berjari-jari r, jika x²+y²<r².
b. Suatu titik A(x,y) terletak pada lingkaran yang berpusat di P(0,0) dan berjari-jari r, jika x²+y²=r².
c. Suatu titik A(x,y) terletak di luar lingkaran yang berpusat di P(0,0) dan berjari-jari r, jika x²+y²>r².
2. Untuk titik pusat lingkaran P(a,b)
a. Suatu titik A(x,y) terletak di dalam lingkaran yang berpusat di P(a,b) dan berjari-jari r, jika (x-a)²+(y-b)²<r².
b. Suatu titik A(x,y) terletak pada lingkaran yang berpusat di P(a,b) dan berjari-jari r, jika (x-a)²+(y-b)²=r².
c. Suatu titik A(x,y) terletak di dalam lingkaran yang berpusat di P(a,b) dan berjari-jari r, jika (x-a)²+(y-b)²>r².
KEDUDUKAN GARIS TERHADAP LINGKARAN
Misalkan g garis dengan persamaan y=ax+b dan L lingkaran dengan persamaan x²+y²=r².
Kedudukan garis g terhadap sebuah lingkaran ditentukan oleh nilai diskriminan (D) yang diperoleh dengan rumus: D=(1+a²)r² – b²
dimana:
D>0 <—> garis g memotong lingkaran di dua titik berlaianan.
D=0 <—> garis g menyinggung lingkaran.
D<0 <—> garis g tidak memotong maupun menyinggung lingkaran.
PERSAMAAN GARIS SINGGUNG LINGKARAN
1. Persamaan Garis Singgung Melalui Suatu Titik pada Lingkaran Berpusat P(0,0) dan Berjari-jari r.
Persamaan garis singgung yang melalui titik (x₁,y₁) pada lingkaran x²+y²=r² adalah: x₁x+y₁y=r²