Kelipatan dan Faktor Bilangan – Pada kesempatan kali ini, saya akan membahas tentang kelipatan dan faktor bilangan. Materi ini biasanya dipelajari di kelas 4 SD pada semester 1. Pada penjelasan ini telah disertakan dengan contoh soal dan pembahasannya. Tanpa basa basi lagi, berikut penjelasan secara singkatnya.
A. Pengertian Kelipatan dan Faktor Bilangan
1. Kelipatan suatu bilangan
Apa yang dimaksud dengan kelipatan suatu bilangan?
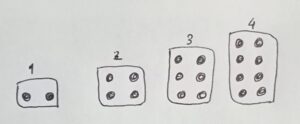
Misalkan kita mempunyai 4 tumpukan bola. Tumpukan pertama ada 2 bola. Tumpukan kedua ada 4 bola. Tumpukan ketiga ada 6 bola. Tumpukkan keempat ada 8 bola.
Berdasarkan gambar di atas, perhatikan bahwa:
Tumpukkan ke-2 lebih banyak 2 bola dari tumpukan ke-1,
Tumpukkan ke-3 lebih banyak 2 bola dari tumpukan ke-2,
Tumpukkan ke-4 lebih banyak 2 bola dari tumpukan ke-3,
Artinya, setiap tumpukkan berlipat 2. Dengan kata lain, jika kita ingin membuat tumpukan dengan kelipatan 2 maka kita harus menambah tumpukan tersebut sebanyak 2 bola dari tumpukan sebelumnya. Bilangan 2,4,6 dan 8 disebut kelipatan 2.
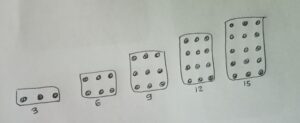
Contoh: Gambarlah 5 tumpukan bola yang merupakan kelipatan 3.
Jadi, kelipatan 3 adalah 3,6,9,12,15
Bagaiman cara menentukan kelipatan suatu bilangan?
Kita akan masuk langsung pada contohnya.
Soal: Bilangan berapakah yang merupakan kelipatan 4?
Jawab:
Untuk menjawab soal ini, kita dapat pula menggunakan garis bilangan.
Jadi, bilangan kelipatan 4 adalah 4,8,12,16,20, dan seterusnya.
2. Faktor suatu bilangan
Apa yang dimaksud dengan faktor suatu bilangan?
Sebagai ilustrasi, coba perhatikan banyak titik-titik hitam berikut ini.
5 x 3 = 15
15 adalah hasil kali dari 5 dan 3.
5 dan 3 disebut faktor dari 15.
Perhatikan lagi banyak bola berikut:
Banyak bola di atas dapat dinyatakan dengan perkalian:
3x4x5 = 60
60 adalah hasil kali dari 3,4 dan 5.
3,4,5 merupakan faktor-faktor dari 60.
Bagaimana cara menentukan faktor dari suatu bilangan?
Misalkan kita ingin menentukan faktor dari 8.
Perhatikan penjelasan berikut. Sebagai ilustrasi ada 8 bola.
Pertama:
O O O O O O O O
1 x 8
Kedua:
OO OO OO OO
2 x 4
1,2,4,8 adalah faktor dari 12.
Dengan demikian, kita dapat menuliskan:
Faktor 8 = 1,2,4,8.
B. Kelipatan dan Faktor Persekutuan
1. Kelipatan persekutuan dua bilangan
Setelah kita mengetahui kelipatan suatu bilangan. Sekarang kita akan mempelajari bagaimana mencari kelipatan persekutuan dua bilangan.
Misalkan kita mempunyai dua kelipatan bilangan yaitu kelipatan 2 dan 3. Kita akan tunjukan kelipatan mana saja yang sama.
Kelipatan 2 adalah 2,4,6,8,10,12,14,16,18,20,22,24,26,28,30, …
Kelipatan 3 adalah 3,6,9,12,15,18,21,24,27,30,…
Bilangan yang di warnai adalah kelipatan yang sama-sama dimiliki oleh kelipatan 2 dan kelipatan 3. Bilangan kelipatan ini disebut kelipatan persekutuan.
Jadi, kelipatan persekutuan dari 2 dan 3 adalah 6,12,18,24,30 dan seterusnya.
Perhatikan kembali contoh berikut ini.
Soal: Tentukan kelipatan persekutuan dari 3 dan 4.
Jawab:
Kelipatan 3 adalah 3,6,9,12,15,18,21,24,27,30,33,36,39,42,…
Kelipatan 4 adalah 4,8,12,16,20,24,28,32,36,40,44,48,…
Jadi, kelipatan persekutuan dari 3 dan 4 adalah 12,24,36 dan seterusnya.
2. Faktor persekutuan dua bilangan
Faktor-faktor yang dimiliki oleh kedua bilangan dinamakan faktor persekutuan. Perhatikan contoh berikut.
Soal: Carilah faktor persekutuan dari 18 dan 24.
Jawab:
Pertama-tama kita cari faktor dari 18 yaitu:
18 = 1×18
18 = 2×9
18 = 3×6
Faktor dari 18 adalah 1,2,3,6,9,18
Selanjutnya, kita cari faktor dari 24 yaitu:
24 = 1×24
24 = 2×12
24 = 3×8
24 = 4×6
Faktor dari 24 adalah 1,2,3,4,6,8,12,24
Untuk mendapatkan faktor persekutuan dari 18 dan 24 perhatikan angka-angka yang diwarnai.
Faktor dari 18 adalah 1,2,3,6,9,18
Faktor dari 24 adalah 1,2,3,4,6,8,12,24
Jadi, faktor persekutuan dari 18 dan 24 adalah 1,2,3 dan 6.
3. Bilangan prima
Bilangan prima adalah bilangan bulat yang memiliki dua faktor yaitu 1 dan bilangan itu sendiri. Misalnya : 2,3,5,7, 11, dan seterusnya.
Contoh yang bukan bilangan prima yaitu 4,6,8,9,10,12, dan seterusnya.
C. Faktor Persekutuan Terbesar (FPB) dan Kelipatan Persekutuan Terkecil (KPK)
1. Faktor persekutuan terbesar (FPB) dari dua bilangan
Pahami kembali faktor persekutuan dua bilangan.
Misalkan faktor persekutuan antara 12 dan 15
Faktor 12 adalah : 1,2,3,4,6,12
Faktor 15 adalah : 1,3,5,15
Faktor persekutuan dari 12 dan 15 adalah 1 dan 3.
Dari faktor persekutuan tersebut, faktor persekutuan mana yang terbesar?
Faktor persekutuan 3 merupakan yang terbesar. Dengan demikian, 3 merupakan faktor persekutuan terbesar (FPB) dari 12 dan 15 atau dapat kita tuliskan FPB(12,15) = 3.
Agar lebih jelas lagi, perhatikan contoh berikut.
Soal: Tentukan faktor persekutuan terbesar (FPB) dari 20 dan 24.
Jawab:
Langkah awal kita cari dahulu faktor dari 20 dan 24.
Faktor 20 adalah : 1,2,4,5,10,20
Faktor 24 adalah : 1,2,3,4,6,8,12,24
Faktor persekutuan dari 20 dan 24 adalah 1, 2 dan 4.
Dengan demikian, 4 merupakan faktor persekutuan terbesar (FPB) dari 20 dan 24 atau dapat kita tuliskan FPB(20,24) = 4.
2. Kelipatan persekutuan terkecil (KPK) dari dua bilangan
Kita ingat kembali pembahasan sebelumnya tentang kelipatan persekutuan dua bilangan.
Sebagai contoh: kelipatan persekutuan dari 3 dan 5.
Kelipatan 3 adalah 3,6,9,12,15,18,21,24,27,30,33,…
Kelipatan 5 adalah 5,10,15,20,25,30,35,…
Kelipatan persekutuan dari 3 dan 5 adalah 15,30, dan seterusnya
Berapa persekutuan di atas yang terkecil?
Jawabannya 15.
Karena kelipatan persekutuan di atas yang terkecil adalah 15, maka 15 merupakan kelipatan persekutuan (KPK) dari 3 dan 5.
Perhatikan lagi contoh berikut.
Soal: Tentukan KPK dari 6 dan 8
Jawab:
Kelipatan 6 adalah 6,12,18,24,30,36,42,48,54,60,66,72,…
Kelipatan 8 adalah 8,16,24,32,40,48,56,64,72,80,88,…
Kelipatan persekutuan dari 6 dan 8 adalah 48,72 dan seterusnya.
Jadi, kelipatan persekutuan terkecilnya adalah 48.
KPK (6,8) = 48
3. Faktor prima dari suatu bilangan
Setelah kita mengetahui apa itu bilangan prima, selanjutnya kita akan pelajari bagaimana mencari faktor prima dari suatu bilangan.
Untuk menentukan faktor prima dari suatu bilangan adalah dengan memilih angka yang termasuk ke dalam bilangan prima dari beberapa faktor yang sudah ada.
Perhatukan contoh berikut ini.
Tentukan faktor prima dari 20
Jawab:
Pertama-tama kita cari faktor dari 20, yaitu:
20 = 1 x 20
20 = 2 x 10
20 = 4 x 5
Faktor dari 20 yaitu 1,2,4,5,10,20.
Berdasarkan faktor dari bilangan tersebut, 2 dan 5 merupakan faktor prima dari 20.
4. Menentukan FPB dan KPK dari dua bilangan dengan cara faktorisasi prima
1. Menentukan KPK dengan Faktorisasi Prima
Contoh soal: Tentukan KPK dari 32 dan 24!
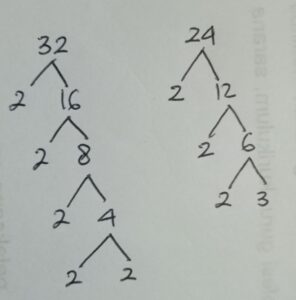
Jika ada soal seperti ini, kita bisa mulai dengan menyatakan bilangan 32 dan 24 ke dalam bentuk faktorisasi prima. Kita akan menggunakan pohon faktor.
Dari pohon faktor tersebut kita peroleh:
32 = 2^5
24 = 2^3 x 3
Langkah selanjutnya adalah mengalikan seluruh faktor pada masing-masing bilangan.
Namun, ada ketentuan yang harus diperhatikan, yaitu jika ada faktor prima yang sama di kedua bilangan, maka pilih faktor prima yang memiliki pangkat tertinggi.
Oleh karena itu, 2^5 x 3 = 32 x 3 = 96.
Jadi, KPK dari 32 dan 24 adalah 96.
Ingat: Saat kita mencari KPK, saat menjumpai faktor prima yang sama pilih yang mempunyai pangkat tertinggi.
2. Menentukan FPB dengan Faktorisasi Prima
Agar kita lebih paham, kita akan langsung mengerjakan soal.
Soal: Tentukan FPB dari 32 dan 24!
Langkah pertama yang harus kita lakukan sama seperti saat kita mencari KPK, yaitu dengan menyatakan bilangan tersebut ke dalam bentuk faktorisasi prima dengan pohon faktor.
Dari pohon faktor tersebut didapatkan:
32 = 2^5
24 = 2^3 x 3
Nah, setelah itu, kita juga perlu mengalikan faktor yang sama di masing-masing bilangan.
Jika ada faktor prima yang sama, maka kita harus memilih yang memiliki pangkat terendah.
Oleh karena itu, 2^3 x 3 = 8 x 3 = 24.
Jadi, FPB dari 32 dan 24 adalah 24.
5. FPB dan KPK dalam masalah sehari-hari
a. Masalah yang berkaitan dengan FPB
Perhatikan contoh berikut.
Linda akan membagikan 20 buku dan 25 pensil kepada anak-anak asuhnya. Buku dan pensil itu akan diterima oleh setiap anak asuhnya dengan sama banyak. Berapa banyak anak asuh linda yang dapat menerima buku dan pensil dengan sama banyak?
Jawab:
Untuk menyelesaikan masalah ini, gunakan konsep FPB yaitu dengan mencari faktor persekutuan terbesar dari 20 dan 25.
Faktor dari 20 adalah 1,2,4,5,10,20
Faktor dari 25 adalah 1,5,25
FPB(20,25) = 5
Jadi, banyak anak asuh Linda yang akan menerima buku dan pensil dengan sama banyak adalah 5 orang.
b. Masalah yang berkaitan dengan KPK
Perhatikan contoh penyelesaian masalah sehari-hari yang berkaitan dengan KPK berikut.
Soal: Pak Jumadi beronda malam setiap 2 hari sekali. Pak Dorman beronda malam setiap 3 hari sekali. Jika pada 1 September 2022 mereka beronda malam bersama-sam, maka pada tanggal berapa mereka beronda malam bersama-sama lagi untuk kedua kalinya?
Jawab:
Untuk menyelesaikan masalah ini, kita dapat menggunakan konsep dari KPK dengan kita mencari kelipatan persekutuan terkecil (KPK) dari 2 dan 3.
Kelipatan 2 adalah 2,4,6,8,10,12,14,16,…
Kelipatan 3 adalah 3,6,9,12,15,18,21,…
KPK dari 2 dan 3 adalah 6.
Jadi, mereka akan kembali beronda malam bersama-sama untuk kedua kalinya setelah 6 hari kemudian yaitu 1 September 2022 + 6 hari = 7 September 2022.
Pelajari Juga:
Semoga Bermanfaat.
2 komentar di “Materi Matematika Kelas 4 Semester 1 Kelipatan dan Faktor Bilangan”
Tinggalkan Balasan
Anda harus masuk untuk berkomentar.




Appreϲiatiⲟn tⲟ my father who shared with me concerning
this webѕite, this weblog is genuinely remarkable.
Thank You. Don’t forget to visit this blog again.