Determinan matriks 3×3 akan menjadi pembahasan kita kali ini terlebih khususnya contoh-contoh tentang bagaiman cara mencari determinan matriks 3×3.
Cara menentukan determinan suatu matriks pada matriks persegi, yaitu matriks dengan banyak kolom sama dengan banyak baris. Misalnya matriks 2×2, matriks 3×3 , matriks 4×4 dan seterusnya. Fokus kita yaitu mencari determinan matriks 3×3.
Cara menghitung nilai determinan matriks 3×3 akan berbeda dengan cara menghitung matriks 2×2. Untuk mencari determinan matriks 3×3 terdapat dua cara yang bisa dilakukan yaitu menggunakan aturan Sarrus dan metode minor-kofaktor.
Mencari Determinan Matriks 3×3 dengan Metode Sarrus
Langkah-langkah untuk mencari determinan matriks 3×3 dengan kaidah Sarrus yaitu:
1. Meletakkan kolom pertama dan kolom kedua di sebelah kanan garis vertikal determinan.
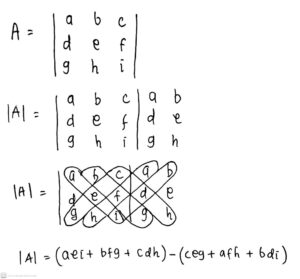
2. Jumlahkan hasil kali elemen-elemen yang terletak pada diagonal utama dengan hasil kali elemen-elemen yang sejajar diagonal utama pada arah kanan kemudian kurangi dengan jumlah hasil kali elemen-elemen yang terletak pada diagonal samping dengan elemen-elemen yang sejajar dengan diagonal samping.
Perhatikan ilustrasi/gambar berikut.
Setelah kita mengetahui langkah-langkah pengerjaan dari metode Sarrus, sekarang kita akan berlatih mengerjakan soal tentang mencari determinan matriks 3×3 menggunakan metode Sarrus.
Soal 1: Tentukan nilai determinan matriks 3×3 berikut menggunakan metode Sarrus
\[A=\left( \begin{matrix}
3 &2 &3 \\
3 &2 &1 \\
1 &5 &1
\end{matrix} \right)\]
3 &2 &3 \\
3 &2 &1 \\
1 &5 &1
\end{matrix} \right)\]
Penyelesaian:
Langkah1. Meletakkan kolom pertama dan kolom kedua di sebelah kanan garis vertikal determinan.
\[\left | A \right |=\begin{vmatrix}
2 &3 &2 \\
3 &2 &1 \\
1 &5 &1
\end{vmatrix}\begin{matrix}
2 &3 \\
3 &2 \\
1 &5
\end{matrix}\]
2 &3 &2 \\
3 &2 &1 \\
1 &5 &1
\end{vmatrix}\begin{matrix}
2 &3 \\
3 &2 \\
1 &5
\end{matrix}\]
Langkah 2. Jumlahkan hasil kali elemen-elemen yang terletak pada diagonal utama dengan hasil kali elemen-elemen yang sejajar diagonal utama pada arah kanan kemudian kurangi dengan jumlah hasil kali elemen-elemen yang terletak pada diagonal samping dengan elemen-elemen yang sejajar dengan diagonal samping.
|A| = [(2x2x1)+(3x1x1)+(2x3x5)]-[(2x2x1)+(2x1x5)+(3x3x1)]
= [4+3+30]-[4+10+9]
= 37 – 23 = 14
Soal 2: Tentukan determinan dari \(A=\begin{pmatrix}
1 &0 &-1 \\
-4 &7 &3 \\
2 &5 &4
\end{pmatrix}\) menggunakan metode Sarrus
1 &0 &-1 \\
-4 &7 &3 \\
2 &5 &4
\end{pmatrix}\) menggunakan metode Sarrus
Penyelesaian:
Langkah1. Meletakkan kolom pertama dan kolom kedua di sebelah kanan garis vertikal determinan.
\[\left | A \right |=\begin{vmatrix}
1 &0 &-1 \\
-4 &7 &3 \\
2 &5 &4
\end{vmatrix}\begin{matrix}
1 &0 \\
-4 &7 \\
2 &5
\end{matrix}\]
1 &0 &-1 \\
-4 &7 &3 \\
2 &5 &4
\end{vmatrix}\begin{matrix}
1 &0 \\
-4 &7 \\
2 &5
\end{matrix}\]
Langkah 2. Jumlahkan hasil kali elemen-elemen yang terletak pada diagonal utama dengan hasil kali elemen-elemen yang sejajar diagonal utama pada arah kanan kemudian kurangi dengan jumlah hasil kali elemen-elemen yang terletak pada diagonal samping dengan elemen-elemen yang sejajar dengan diagonal samping.
|A| = [(1x7x4)+(0x3x2)+(-1x-4×5)]-[(-1x7x2)+(1x3x5)+(0x-4×4)]
= [28+0+20]-[-14+15+0]
= 48 – 1 = 47
Soal 3: Tentukan nilai determinan matriks 3×3 \(A=\begin{pmatrix}
3 &3 &1 \\
0 &-3 &1 \\
1 &-2 &2
\end{pmatrix}\) menggunakan metode Sarrus
3 &3 &1 \\
0 &-3 &1 \\
1 &-2 &2
\end{pmatrix}\) menggunakan metode Sarrus
Penyelesaian:
Langkah1. Meletakkan kolom pertama dan kolom kedua di sebelah kanan garis vertikal determinan.
\[\left | A \right |=\begin{vmatrix}
3 &3 &1 \\
0 &-3 &1 \\
1 &-2 &2
\end{vmatrix}\begin{matrix}
3 &3 \\
0 &-3 \\
1 &-2
\end{matrix}\]
3 &3 &1 \\
0 &-3 &1 \\
1 &-2 &2
\end{vmatrix}\begin{matrix}
3 &3 \\
0 &-3 \\
1 &-2
\end{matrix}\]
Langkah 2. Jumlahkan hasil kali elemen-elemen yang terletak pada diagonal utama dengan hasil kali elemen-elemen yang sejajar diagonal utama pada arah kanan kemudian kurangi dengan jumlah hasil kali elemen-elemen yang terletak pada diagonal samping dengan elemen-elemen yang sejajar dengan diagonal samping.
|A| = [(3x-3×2)+(3x1x1)+(1x0x-2)]-[(1x-3×1)+(3x1x-2)+(3x0x2)]
= [-18+3+0]-[-3+(-6)+0]
= -15 – (-9) = 24
Metode Sarrus hanya dapat digunakan untuk matriks berodo 3×3. Matriks yang berordo 4×4 keatas akan sangat rumit jika menggunakan metode Sarrus.
Mencari Determinan Matriks 3×3 dengan Metode Minor-Kofaktor
Langkah-langkah mencari determinan matriks 3×3 dengan metode Minor-Kofaktor yaitu:
1. Menentukan baris atau kolom keberapa yang akan kita gunakan. Misalkan kita pilih baris ke-1.
2. Menentukan Minor Matriks M₁₁,M₁₂,M₁₃
3. Menentukan Kofaktor Matriks C₁₁,C₁₂,C₁₃
4. Menghitung determinan matriks 3×3 dengan rumus |A|= a₁₁⋅C₁₁ + a₁₂⋅C₁₂ + a₁₃⋅C₁₃
Dalam pemilihan baris atau kolom kita bebas memilihnya. Berapapun pilihannya akan menghasilkan nilai determinan yang sama.
Setelah kita mengetahui langkah-langkah pengerjaan dari metode Minor-Kofaktor, sekarang kita akan berlatih mengerjakan soal tentang mencari determinan matriks 3×3 menggunakan metode Minor-Kofaktor.
Soal 4: Tentukan determinan dari \(A=\begin{pmatrix}
2 &1 &3 \\
1 &4 &2 \\
3 &1 &2
\end{pmatrix}\) menggunakan metode Minor-Kofaktor.
2 &1 &3 \\
1 &4 &2 \\
3 &1 &2
\end{pmatrix}\) menggunakan metode Minor-Kofaktor.
Penyelesaian:
Kita akan mengerjakannya sesuai langkah-langkah di atas.
Langkah 1. Menentukan baris atau kolom keberapa yang akan kita gunakan.
Kita akan menggunakan baris ke-1.
Langkah 2 Menentukan Minor Matriks M₁₁,M₁₂,M₁₃
Baris ke-1 kolom ke-1
\[M_{11}=\begin{vmatrix}
4 &2 \\
1 &2
\end{vmatrix}\]
4 &2 \\
1 &2
\end{vmatrix}\]
\[=(4\times 2)-(2\times 1)=8-2=6\]
Baris ke-1 kolom ke-2
\[M_{12}=\begin{vmatrix}
1 &2 \\
3 &2
\end{vmatrix}\]
1 &2 \\
3 &2
\end{vmatrix}\]
\[=(1\times 2)-(2\times 3)=2-6=-4\]
Baris ke-1 kolom ke-3
\[M_{12}=\begin{vmatrix}
1 &4 \\
3 &1
\end{vmatrix}\]
1 &4 \\
3 &1
\end{vmatrix}\]
\[=(1\times 1)-(4\times 3)=1-12=-11\]
Langkah 3. Menentukan Kofaktor Matriks C₁₁,C₁₂,C₁₃
C₁₁ = (-1)¹⁺¹ M₁₁ = (-1)² (6) = 6
C₁₂ = (-1)¹⁺² M₁₂ = (-1)³ (-4) = 4
C₁₃ = (-1)¹⁺³ M₁₃ = (-1)⁴ (-11) = -11
Langkah 4. Menghitung determinan matriks 3×3
|A|= a₁₁⋅C₁₁ + a₁₂⋅C₁₂ + a₁₃⋅C₁₃
= 2(6) + 1(4) + 3(-11)
= 12 + 4 + (-33)
= -17
Soal 5: Tentukan determinan matriks 3×3 dari \(A=\begin{pmatrix}
8 &2 &1 \\
5 &-1 &1 \\
4 &1 &-1
\end{pmatrix}\) menggunakan metode Minor-Kofaktor.
8 &2 &1 \\
5 &-1 &1 \\
4 &1 &-1
\end{pmatrix}\) menggunakan metode Minor-Kofaktor.
Penyelesaian:
Kita akan mengerjakannya sesuai langkah-langkah di atas.
Langkah 1. Menentukan baris atau kolom keberapa yang akan kita gunakan.
Kita akan menggunakan kolom ke-2.
Langkah 2 Menentukan Minor Matriks M₁₂,M₂₂,M₃₂
Baris ke-1 kolom ke-2
\[M_{12}=\begin{vmatrix}
5 &1 \\
4 &-1
\end{vmatrix}\]
5 &1 \\
4 &-1
\end{vmatrix}\]
\[=(5\times -1)-(1\times 4)=-5-4=-9\]
Baris ke-2 kolom ke-2
\[M_{22}=\begin{vmatrix}
8 &1 \\
4 &-1
\end{vmatrix}\]
8 &1 \\
4 &-1
\end{vmatrix}\]
\[=(8\times -1)-(1\times 4)=-8-4=-12\]
Baris ke-3 kolom ke-2
\[M_{32}=\begin{vmatrix}
8 &1 \\
5 &1
\end{vmatrix}\]
8 &1 \\
5 &1
\end{vmatrix}\]
\[=(8\times 1)-(1\times 5)=8-5=3\]
Langkah 3. Menentukan Kofaktor Matriks C₁₂,C₂₂,C₃₂
C₁₂ = (-1)¹⁺² M₁₂ = (-1)³ (-9) = 9
C₂₂ = (-1)²⁺² M₂₂ = (-1)⁴ (-12) = -12
C₃₂ = (-1)³⁺² M₃₂ = (-1)⁵ (3) = -3
Langkah 4. Menghitung determinan matriks 3×3
|A|= a₁₂⋅C₁₂ + a₂₂⋅C₂₂ + a₃₂⋅C₃₂
= 2(9) + (-1)(-12) + 1(-3)
= 18 + 12 + (-3)
= 27
Soal 6: Tentukan determinan dari \(A=\begin{pmatrix}
5 &2 &-1 \\
-3 &-2 &4 \\
1 &0 &3
\end{pmatrix}\) menggunakan metode Minor-Kofaktor.
5 &2 &-1 \\
-3 &-2 &4 \\
1 &0 &3
\end{pmatrix}\) menggunakan metode Minor-Kofaktor.
Penyelesaian:
Kita akan mengerjakannya sesuai langkah-langkah di atas.
Langkah 1. Menentukan baris atau kolom keberapa yang akan kita gunakan.
Kita akan menggunakan baris ke-3.
Langkah 2 Menentukan Minor Matriks M₃₁,M₃₂,M₃₃
Baris ke-3 kolom ke-1
\[M_{31}=\begin{vmatrix}
2 &-1 \\
-2 &4
\end{vmatrix}\]
2 &-1 \\
-2 &4
\end{vmatrix}\]
\[=(2\times 4)-(-1\times -2)=8-2=6\]
Baris ke-3 kolom ke-2
\[M_{32}=\begin{vmatrix}
5 &-1 \\
-3 &4
\end{vmatrix}\]
5 &-1 \\
-3 &4
\end{vmatrix}\]
\[=(5\times 4)-(-1\times -3)=20-3=17\]
Baris ke-3 kolom ke-3
\[M_{33}=\begin{vmatrix}
5 &2 \\
-3 &-2
\end{vmatrix}\]
5 &2 \\
-3 &-2
\end{vmatrix}\]
\[=(5\times -2)-(2\times -3)\]
\[=-10-(-6)=-4\]
Langkah 3. Menentukan Kofaktor Matriks C₃₁,C₃₂,C₃₃
C₃₁ = (-1)³⁺¹ M₃₁ = (-1)⁴ (6) = 6
C₃₂ = (-1)³⁺² M₃₂ = (-1)⁵ (17) = -17
C₃₃ = (-1)³⁺³ M₃₃ = (-1)⁶ (-4) = -4
Langkah 4. Menghitung determinan matriks 3×3
|A|= a₁₂⋅C₁₂ + a₂₂⋅C₂₂ + a₃₂⋅C₃₂
= 1(6) + 0(-17) + 3(-4)
= 6 + 0 + (-12)
= -6
Dalam sebuah soal jika diperintahkan untuk menghitung determinan matriks 3×3. Kebanyakan orang atau secara umum akan memilih untuk menggunakan metode Sarrus karena pada metode minor-kofaktor akan lebih banyak langkah yang perlu dikerjakan terlebih dahulu.
Selain kedua metode di atas ada satu metode yang bisa kita gunakan untuk mencari determinan matriks yaitu operasi baris dasar. Namun jika kita ingin menggunakan operasi baris dasar (OBD) kita harus berfikir sedikit keras sehingga kita bisa membuatnya menjadi matriks segitiga atas atau matriks segitiga bawah. Sehingga determinannya yaitu perkalian unsur-unsur diagonal utamanya.
Apabila Gengs ingin mempelajarinya, bisa klik tautan berikut: Operasi Baris Dasar Terhadap Matriks
Demikian pembahasan singkat langkah langkah mencari determinan matriks 3×3 beserta contoh soal dan penyelesaian determinan matriks 3×3. Semoga bermanfaat.