Contoh Soal dan Penyelesaian Logika Matematika

Hayy Hayy Hayy Hallo Hallo Hallo….
Apa kabar hari ini? Semoga sehat selalu yaaaa

Pada kesempatan kali ini, saya akan memberikan lagi beberapa contoh dan penyelesaian dari logika matematika. Bagi teman-teman yang kurang paham materi tentang “Logika Matematika”, teman-teman bisa latihan dari contoh-contoh soal yang saya bagikan kali ini.

Sebelum mencoba mengerjakan soal-soalnya, ada baiknya Gengs pelajari terlebih dahulu materinya.

Bagian 1 Proposisi dan Tabel Kebenaran

Jangan Lupa, Baca Juga
Implikasi Dan Biimplikasi Dalam Logika Matematika
Konjungsi Dan Disjungsi Dalam Logika Matematika

Nomor 1
Soal: Diketahui proposisi q—>r bernilai salah. Tentukan nilai kebenaran dari (pvq)—>r
Jawab:
Proposisi  q—>r bernilai salah jika dan hanya jika q benar dan r salah.
Tabel kebenaran memberikan sebagai berikut

Terlihat bahwa proposisi (p v q) —> r bernilai salah.

Nomor 2
Soal: Jika proposisi p <–> q bernilai salah, tentukan nilai kebenaran dari proposisi (p v q) —> (p ^ q)
Jawab:
Proposisi p <–> q bernilai salaj jika dan hanya jika p dan q memiliki nilai kebenaran yang berbeda, sehingga dapat memberikan tabel kebenaran sebagai berikut

Jadi (p v q) —> (p ^ q) bernilai salah.

Nomor 3
Soal: Diketahui proposisi p v (p ^ q) bernilai benar. Tentukan nilai kebenaran dari:
(a) Proposisi p
(b) Proposisi -p ^ q
Jawab:
(a) Apabila dikerjakan berdasarkan dalil penghapusan, maka akan diperoleh sebagai berikut:
p v (p ^ q) = p
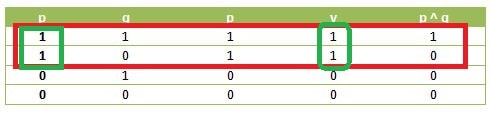
Dengan demikian proposisi p bernilai benar. Atau apabila disajikan dalam tabel kebenaran akan tampak sebagai berikut:

dari tabel yang diberikan di atas. Dapat dilihat bahwa p v (p ^ q) bernilai benar maka p bernilai benar (perhatikan kotak yang diberi warna hijau).

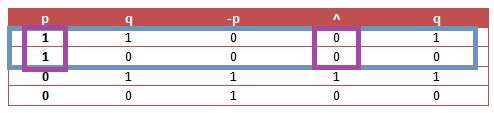
(b) Dengan tabel kebenaran dapat di peroleh sebagai berikut:

dari tabel yang diberikan di atas. Dapat dilihat bahwa -p  ^ q bernilai salah maka p bernilai benar (perhatikan kotak yang diberi warna ungu).

Bagian 2 Dalil Kesetaraan

Nomor 1
Soal: Dengan menggunakan dalil kesetaraan, buktikan bahwa [(p –> -p) ^ -p] –> -p adalah suatu tautologi.
Jawab:
[(p –> -p) ^ -p] –> -p 
= [(-p v -p) ^ -p] –> -p
=(-p ^ -p) –> -p
= p v -p
= i 

Nomor 2
Soal: Dengan menggunakan dalil kesetaraan, buktikan bahwa proposisi [(q –> p) ^ q] –> p adalah suatu tautologi.
Jawab:
[(q –> p) ^ q] –> p
= – [(-q v p) ^ q] v p
= (q ^ -p) v -q v p
= (q v -q v p) ^ (-p v -q v p)
= (i v p) ^ (i v -q)
= i ^ i
= i

Nomor 3
Soal: Dengan menggunakan dalil-dalil kesetaraan, periksa apakah proposisi berikut tautologi:

Jawab:
[-(p v q) v (-p ^ q)] –> -p
= [(-p ^ -q) v (-p ^ q)] –> -p
= [-p ^ (-q v q)] –> -p
= (-p ^ i) –> -p
= -p –> -p
= p v -p
= i

Bagian 3 Argumen


Jangan Lupa, Baca Juga
Penarikan Kesimpulan Dalam Logika Matematika

Nomor 1
Soal: Diberikan argumen sebagai berikut. Jika Iis dan Ees berada di lobi asrama maka keduanya sedang belajar pelajaran matematika. Ternyata, setidaknya ada satu orang yang tidak sedang belajar pelajaran matematika, Dapat disimpulkan bahwa setidaknya ada satu orang yang tidak berada di lobi asrama.
Tentukan:
(a) Lambangkan argumen diatas
(b) Periksa kesahan argumen di atas dengan menggunakan dalil-dalil kesetaraan
Jawab:
(a) Misalkan:
p : Iis berada di lobi asrama
q : Ees berada di lobi asrama
r : Iis sedang belajar pelajaran matematika
s : Ees sedang belajar pelajaran matematika

Argumen:

H1: (p ^ q) –> (r ^ s)
H2: -r v -s
—————————
K : -p v -q

(b) Dengan dalil-dalil kesetaraan diperoleh sebagai berikut:

(H1 ^ H2) –> K
= -(H1 ^ H2) v K
= -H1 v -H2 v K
= -[(p ^ q) –> (r ^ s)] v (r ^ s) v -(p ^ q)
= -[-(p ^ q) v (r ^ s)] v (r ^ s) v -(p ^ q)
= [(p ^ q) ^ -(r ^ s)] v -[-(r ^ s) ^ (p ^ q)]
= t v -t ; dengan t = [(p ^ q) ^ -(r ^ s)]
= i
Karena implikasinya merupakan tautologi maka argumen tersebut sah.

Nomor 2
Soal: Perhatikan argumen berikut. Jika Ana di terima di salah satu sekolah menengah atas maka Ana belajar matematika enam jam perhari. Jika Ana belajar matematika enam jam perhari maka Ana lulus mata pelajaran matematika. Ternyata Ana belajar matematika enam jam per hari. Kesimpulannya, Ana lulus mata pelajaran matematika. Dengan menggunakan dalil-dalil kesetaraan, periksa kesahan argumen tersebut.
Jawab:
Misalkan:
p : Ana diterima di salah satu sekolah menengah atas
q : Ana belajar matematika enam jam perhari
r : Ana lulus mata pelajaran matematika

Argumen:

H1: p –> q
H2: q –> r
H3: q
—————-
K  : r

Setelah menentukan argumennya, selanjutnya akan diperiksa argumen dengan dalil-dalil kesetaraan:
[(p –> q) ^ (q –> r) ^ q] –> r
= [(-p v q) ^ (-q v r) ^ q] –> r
= [(-p v q) ^ q ^ (-q v r)] –> r
= [q ^ (-q v r)] –> r
= [(q v -q) v (q ^ r)] –> r
= [o v (q ^ r)] –> r
= (q ^ r) –> r
= -(q ^ r) v r
= (-q v -r) v r
= -q v (-r v r)
= -q v i
= i
Karena implikasinya merupakan tautologi maka argumen tersebut sah.

Untuk contoh soal dan penyelesaian lainnya tentang Logika Matematik, teman-teman dapat klik link di bawah ini.
Soal Dan Jawaban – Modus Ponens, Modus Tollens Dan Silogisme
Contoh Soal Proposisi Dan Tabel Kebenaran Beserta Jawabannya
Contoh Soal dan Jawaban Logika Matematika
Soal Dan Jawaban – Konjungi Dan Disjungi

Demikian Contoh Soal dan Penyelesaian Logika Matematika. Semoga bermanfaat.