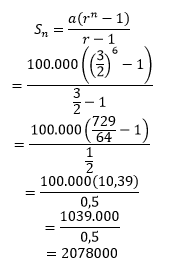Pertumbuhan dan Peluruhan – Materi ini merupakan penerapan dari konsep barisan dan deret. Jadi, Gengs harus sudah menguasai materi tentang barisan dan deret. Baik itu barisan dan deret pada aritmetika dan barisan dan deret pada geometri. Barisan aritmetika kita gunakan untuk menghitung bunga tunggal sedangkan barisan geometri kita gunakan untuk menghitung bunga majemuk, pertumbuhan dan peluruhan.
Berikut ini akan diberikan beberapa contoh soal mulai tentang aplikasi dari barisan dan deret baik itu pada pertumbuhan dan peluruhan, bunga tunggal dan bunga majemuk.
Soal 1
Bakteri membela menjadi 2 bagian setiap 2 jam sekali. Jika pada pukul 07.00 Banyak bakteri 350 ekor, tentukan. Banyak bakteri pada pukul 17.00 untuk hari yang sama yaitu…
Jawab:
Karena pada kasus tersebut diketahui bahwa bakteri membela menjadi 2 bagian, maka kasus ini merupakan kasus barisan geometri.
Diketahui:
U₁=a=350
Rasio=r=2
Banyak suku= 10 jam/2jam=5 (dari jam 07.00 hingga 17.00 bakteri telah membela sebanyak 5 kali)
U₁₇₀₀=a$r^n$ = 350(2⁵)=11200
Jadi, banyak bakteri pada pukul 17.00 adalah 11200 ekor
Soal 2
Produksi sarung tangan setiap minggunya bertambah dengan jumlah yang tetap. Jika jumlah produksi sarung tangan sampai minggu ke-5 adalah 1250 pasang dan jumlah produksi sampai minggu ke-10 adalah 3125 pasang, tentukan jumlah produksi sarung tangan sampai minggu ke-20…
Jawab:
Karena jumlah pertambahan produksi sarung tangan selalu tetap setiap minggunya dan diketahui jumlah produksi sarung tangan sampai minggu ke-5 dan ke-10, maka kasus tersebut merupakan kasus deret aritmetika.
Diketahui:
S₅=1250
S₁₀=3125
\(S_n\)=n/2 [2a+(n-1)b]
S₅=5/2 [2a+(5-1)b]
1250=5/2 [2a+4b]
1250=5a+10b ……. Pers1
S₁₀=10/2 [2a+(10-1)b]
S₁₀=10/2 [2a+9b]
3125=5[2a+9b]
3125=10a+45b …… pers2
Eliminasikan pers1 dan pers2
5a+10b=1250
10a+45b=3125
Persamaan pertama dikali 2 dan persamaan kedua dikali 1
10a+20b=2500
10a+45b=3125
Kurangkan kedua persamaan tersebut
-25b=-625
b=25
Substitusika b=25 kedalam persamaan pertama
5a+10b=1250
5a+10(25)=1250
5a+250=1250
5a=1000
a=200
Jumlah sampai minggu ke-20
\(S_n\)=n/2 [2a+(n-1)b]
S₂₀=20/2 [2a+(20-1)b]
=10[2(200)+19(25)]
=10[400+475]
=8750
Jadi, jumlah produksi sarung tangan sampai minggu ke-20 adalah 8750 pasang.
Soal 3
Pada pukul 18.00 massa suatu zat radioaktif adalah 0,5 kg. Apabila laju peluruhan zat radioaktif tersebut 2% setiap jam, hitunglah sisa zat radioaktif pada pukul 20.00!
Jawab:
t = 2 jam [lamanya peluruhan dari pukul 18.00 hingga 20.00]
P₀ = 0,5 [massa mula-mula zat radioaktif]
P = 2% = 0.02 laju peluruhan setiap jam
Dengan demikian,
Pt = P₀ (1-P)ᵗ
P₂ = 0,5(1-0,02)²
= 0,5(0,98)²
= 0,9604
Jadi, sisa zat radioaktif setelah 2 jam peluruhan yaitu 0,9604 kg.
Soal 4
Seorang karyawan pada bulan pertama ia masuk kerja di suatu perusahaan memperoleh gaji sebesar Rp3.100.000. Setiap 4 bulan sekali, gajinya akan dinaikkan sebesar Rp115.ooo. Tentukan besar gaji perbulan seorang karyawan setelah bekerja selama 7 tahun di perusahaan tersebut.
Jawab:
Karena setiap 4 bulan sekali gaji karyawan tersebut akan dinaikkan dengan kenaikan tetap sebesar Rp115.000.
Contoh ini merupakan contoh barisa aritmetika karena gaji karyawan tersebut akan dinaikkan dengan kenaikan tetap.
Diketahui:
U₁=a=3.100.000
b=115.000
Karena kenaikan setiap 4 bulan sekali maka dalam 1 tahun mengalami 3 kali kenaikan. Dengan demikian dalam 7 tahun terjadi 21 kali kenaikan.
U₇=a+21b
=3.100.000+21(115.000)
=3.100.000+2.415.000
=5.515.000
Jadi, besar gaji karyawan tersebut setelah bekerja selama 7 tahun adalah Rp5.515.000
Soal 5
Sebuah kendaraan roda empat dibeli dengan harga Rp.200.000.000. Jika setiap tahun harganya mengalami penurunan 20% dari nilai tahun sebelumnya, maka tentukanlah harga kendaraan roda empat itu setelah dipakai selama 5 tahun.
Jawab:
Diketahui :
Mo = 200.000.000 [harga awal membeli kendaraan tersebut]
i = 20% = 0,2 [mengalami penurunan dari tahun sebelumnya]
n = 5 [telah digunakan selama 5 tahun]
Ditanya: Mn ?
Jawab
Mn = M₀ \((1 – i)^n\)
M₅ = 200.000.000 (1 – 0,2)⁵
M₅ = 200.000.000 (0,8)⁵
M₅ = 200.000.000(0,32768)
M₅ = 65.536.000
Soal 6
Populasi penduduk di suatu pulau setiap tahun 3/2 kali lipat. Jika populasi penduduknya saat ini 100.000 jiwa, maka 6 tahun yang akan datang populasinya sama dengan?
Jawab:
r=3/2
a=100.000
n=6
dengan demikian,
Jadi, populasi 6 tahun yang akan datang adalah 2078000 (apabila dibulatkan dua angka di belakang koma).
Demikian contoh soal pertumbuhan dan peluruhan.
Semoga Bermanfaat.