Pada kesempatan kali ini, saya akan memberikan 20 nomor contoh soal matematika kelas 10 semester 2. Bukan hanya contoh soal, saya pun akan memberikan pembahasannya. Materi-materi diantaranya: 1) Sistem persamaan dan pertidaksamaan linear, 2) Fungsi kuadrat, 3) Statistika dan 4) Peluang. Tanpa berlama-lama lagi, berikut 20 contoh soal matematika kelas 10 semester 2.
Soal 1
Sebuah pertunjukan memberlakukan dua harga tiket masuk. Harga tiket untuk dewasa sebesar Rp 100.00,00 dan harga tiket untuk anak-anak sebesar Rp 40.000,00. Pada suatu hari, terdapat 300 orang datang menyaksikan pertunjukan tersebut dengan pendapatan sebesar Rp 19.200.000,00. Jumlah orang dewasa dan anak-anak yang datang ke pertunjukan pada hari itu adalah…
Pembahasan:
Misalkan:
x=jumlah orang dewasa yang datang
y=jumlah anak-anak yang datang
1) Pertunjukan disaksikan oleh 300 orang diperoleh persamaan:
x + y=300 (1)
2) Jumlah pendapatan pada hari itu sebesar Rp 19.200,00 diperoleh persamaan:
100.000x + 40.000y = 19.200.000
100x + 40y = 19.200
5x + 2y = 960 (2)
Eliminasi y dari persamaan (1) dan (2)
x+y=300 |x2| 2x+2y=600
5x+2y=960 |x1| 5x+2y=960
—————– –
-3x = -360
3x = 360
x = 120
Substitusikan x = 120 ke dalam persamaan (1).
x+y=300
120+y=300
y=180
Jadi, pertunjukkan tersebut disaksikan oleh 120 orang dewasa dan 180 anak-anak.
Soal 2
Pada tahun 2009, umur Pak Joko lima kali umur anaknya. Pada tahun 2015, umur Pak Joko tiga kali umur anaknya. Umur Pak Joko tahun 2019 adalah…
Pembahasan:
Misalkan:
x =umur pak Joko pada tahun 2019
y =umur anak pak Joko pada tahun 2019
1) Pada tahun 2009, umur pak Joko lima kali umur anaknya maka diperoleh persamaan:
(x-10) = 5(y-10)
x-10 = 5y-50
x = 5y-40 (1)
2) Pada tahun 2015, umur Pak Joko tiga kali umur anaknya maka diperoleh persamaan:
(x-4) = 3(y-4)
x-4 = 3y-12
x = 3y-8 (2)
Dari persamaan (1) dan (2) diperoleh hubungan:
5y-40=3y-8
5y-3y=40-8
2y=32
y=16
Substitusikan y=16 dalam persamaan (2):
x=3y-8
x=3(16)-8
x=48-8
x=40
Jadi, umur Pak Joko pada tahun 2019 adalah 40 tahun.
Soal 3
Di suatu toko kue, Aji, Bintang dan Candra membeli pisang goreng, donat dan roti. Aji membeli 2 pisang goreng, 1 donat, dan 2 roti seharga Rp 24.000,00. Bintang membeli 1 pisang goreng, 3 donat dan 1 roti seharga Rp 22.000,00. Candra membeli 3 pisang goreng, 2 donat dan 1 roti seharga Rp 23.000,00. Harga 2 pisang goreng, 3 donat dan 2 roti adalah…
Pembahasan:
Misalkan:
x=harga 1 pisang goreng
y=harga 1 donat
z=harga 1 roti
1) Aji membeli 2 pisang goreng, 1 donat dan 2 roti seharga Rp 24.000,00 diperoleh persamaan:
2x+y+2z=24.000 (1)
2) Bintang membeli 1 pisang goreng, 3 donat dan 1 roti seharga Rp 22.000,00 diperoleh persamaan:
1x+3y+1z=22.000 (2)
3) Candra membeli 3 pisang goreng, 2 donat dan 1 roti seharga Rp 23.000,00 diperoleh persamaan:
3x+2y+1z=23.000 (3)
Eliminasi z dari persamaan (1) dan (2)
2x+y+2z=24.000 |x1| 2x+y+2z=24.000
1x+3y+1z=22.000 |x2| 2x+6y+2z=44.000
——————- –
-5y = -20.000
y = 4.000
Eliminasi z dari persamaan (2) dan (3)
1x+3y+1z=22.000
3x+2y+1z=23.000
———————— –
-2x + y = -1.000
-2x + 4.000 = -1.000
-2x = -5.000
x = 2.500
Substitusikan x=2.500 dan y=4.000 ke dalam persamaan (1).
2x+y+2z=24.000
2(2.500) + 4.000 + 2z = 24.000
5.000 + 4.000 + 2z = 24.000
9.000 + 2z = 24.000
2z = 15.000
z = 7.500
Harga 2 pisang goreng, 3 donat dan 2 roti
= 2x+3y+2z
= 2(2.500) + 3(4.000) + 2(7.500)
= 5.000 + 12.000 + 15.000
= 32.000
Jadi, harga 2 pisang goreng, 3 donat dan 2 roti adalah Rp 32.000,00
Soal 4
Perhatikan gambar berikut.

Sistem pertidaksamaan yang sesuai dengan daerah arsiran adalah…
Pembahasan:
1) Persamaan garis yang melalui titik (4,0) dan (0,8) yaitu 2x+y=8.
Cek titik (0,0) kedalam 2x+y
2(0)+0=0≤8 sehingga pertidaksamaan 2x+y≤8
2) Persamaan garis yang melalui titik (6,0) dan (0,4) yaitu 2x+3y=12.
Cek titik (0,0) kedalam 2x+3y
2(0)+3(0)=0≤12 sehingga pertidaksamaan 2x+3y≤12
3) daerah arsiran terletak di kanan sumbu Y sehingga x≥0.
4) Daerah arsiran terletak di atas sumbu X sehingga y≥0
Jadi, sistem pertidaksamaannya adalah 2x+y≤8; 2x+3y≤12;x≥;y≥0.
Soal 5
Diketahui daerah penyelesaian sistem pertidaksamaan berikut.

Nilai minimum daerah penyelesaian sistem pertidaksamaan untuk fungsi objektif f(x,y) = 3x + 5y adalah…
Pembahasan:
Garis lurus pertama melalui titik (0,15) dan (40,0). Diperoleh persamaan:
15x+40y=600
3x+8y=120 (1)
Garis lurus kedua melalui titik (0,22.5) dan (22.5,0). Diperoleh persamaan:
22,5x+22,5y=506,25
x+y=22,5 (2)
Titik potong persamaan (1) dan (2) sebagai berikut.
3x+8y=120 |x1| 3x+8y=120
x+y=22,5 |x8| 8x+8y=180
———— –
-5x = -60
x = 12
Substitusikan x=12 ke dalam persamaan (2)
x+y=22,5
12+y=22,5
y = 10,5
Uji titik pojok
| Titik Pojok | Nilai f(x,y)=3x+5y |
| (0, 22.5) | 3(0)+5(22,5)=112,5 |
| (40,0) | 3(40)+5(0)=120 |
| (12, 10.5) | 3(12)+5(10,5)=88,5 |
Diperoleh nilai minimum 88,5.
Jadi, nilai minimumnya adalah 88,5.
Soal 6
Grafik fungsi y = (m – 2)x² + 4x + (m – 5) menyinggung sumbu x. Nilai m yang memenuhi adalah…
Pembahasan:
Pada fungsi y = (m – 2)x² + 4x + (m – 5) diketahui a=(m-2), b=4 dan c=(m-5).
Syarat grafik fungsi menyinggung sumbu X yaitu D=0.
Dengan demikian:
b²-4ac=0
4²-4(m-2)(m-5)=0
16-4(m-2)(m-5)=0
-4(m-2)(m-5)=-16
(m-2)(m-5)=4
m²-7m+10=4
m²-7m+6=0
(m-1)(m-6)=0
m =1 atau m=6
Jadi, nilai m yang memenuhi adalah 1 atau 6.
Soal 7
Perhatikan gambar fungsi f(x) = ax² + bx + c berikut.
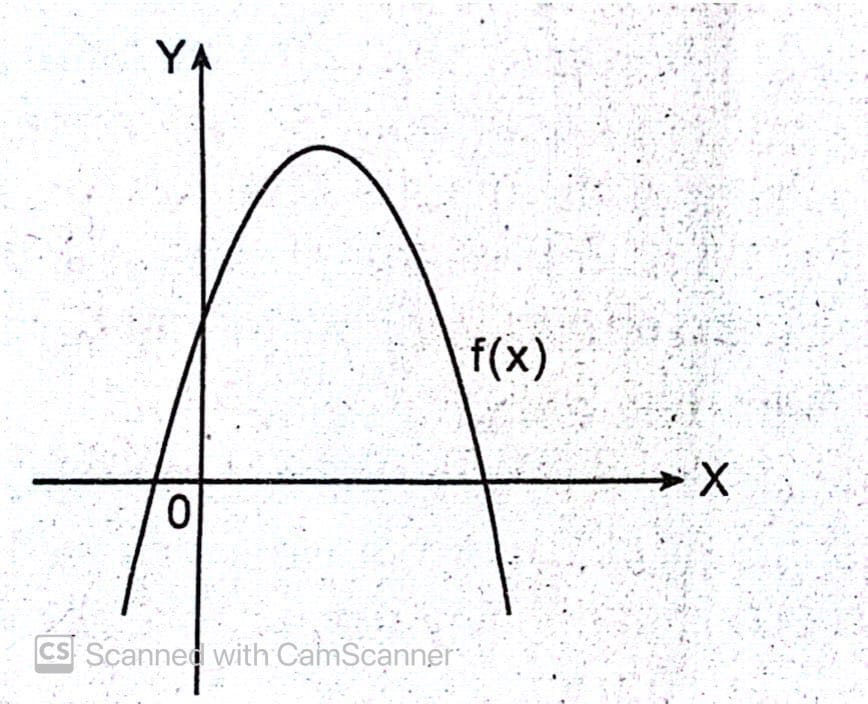
1) Nilai a
Oleh karena bentuk grafik membuka ke bawah maka a bernilai negatif atau a<0. 2)Nilai b Ditinjau dari sumbu simetrinya yaitu x=-b/2a. Sumbu simetri berada di sebelah kanan sumbu Y maka x bernilai positif. Oleh karena a<0(negatif) maka b haruslah positif atau b>0.
3) Nilai c
Nilai c dapat ditinjau dari perpotongan grafik terhadap sumbu Y. Oleh karena perpotongan terletak di atas sumbu X maka nilai c>0.
Jadi, nilai a,b dan c yang sesuai adalah a<0,b>0 dan c>0.
Soal 8
Perhatikan grafik fungsi kuadrat berikut.
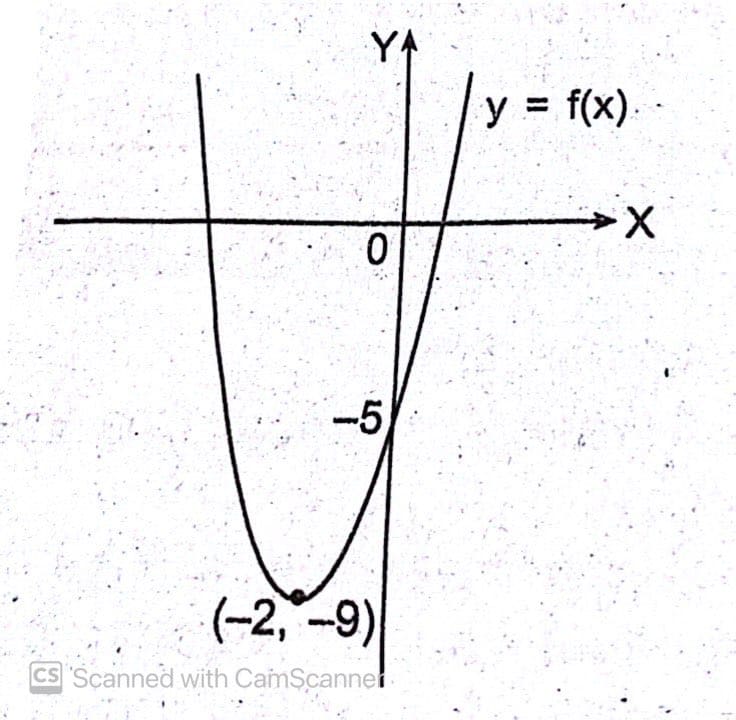
Koordinat titik potong grafik dengan sumbu x adalah…
Pembahasan:
Grafik fungsi melalui titik puncak (p,q) = (-2,-9).
1) Persamaan fungsi:
y=a(x-p)²+q
=a(x-(-2))²-9
=a(x+2)²-9
2) Grafik fungsi juga melalui titik (0,-5) maka:
y=a(x+2)²-9
-5=a(0+2)²-9
-5=a(2)²-9
-5=4a-9
4a=4
a=1
diperoleh y=(x+2)² – 9
3) Titik potong dengan sumbu x:
y = (x+2)² – 9
0 = (x+2)² – 9
(x+2)² = 9
x+2=3 atau x+2=-3
x=1 atau x=-5
Jadi, koordinat titik potongnya adalah (-5,0) dan (1,0).
Pelajari Juga:
1. Contoh Soal dan Jawaban Fungsi Kuadrat SMA
2. Contoh Soal dan Pembahasan Fungsi Kuadrat
Soal 9
Diketahui fungsi kuadrat f(x) = (n-3)x² + nx – 1. Jika f(x) definit negatif, nilai n yang memenuhi adalah …
Pembahasan:
Syarat definit negatif:
1)a<0
n-3<0
n<3
2)D<0
b²-4ac<0
n²-4(n-3)(-1)<0
n²+4n-12<0
(n-2)(n+6)<0
-6<n<2
Berdasarkan 1) dan 2) maka nilai n yang memenuhi -6<n<2.
Jadi, nilai n yang memenuhi adalah -6<n<2.
Soal 10
Tabel berikut menyatakan hasil penilaian guru terhadap kemampuan pelajaran Matematika dari 70 orang siswa.
| Nilai | Frekuensi |
| 34-38 | 5 |
| 39-43 | 9 |
| 44-48 | 14 |
| 49-53 | 20 |
| 54-58 | 16 |
| 59-63 | 6 |
Modus dari data pada tabel di atas adalah …
Pembahasan:
Pada tabel, kelas modus dimiliki oleh kelas interval yang memiliki frekuensi tertinggi.
Dari tabel terlihat, frekuensi tertinggi dimiliki kelas interval 49-53 sehingga diperoleh:
Lₒ=49-0,5=48,5
p=53-49+1=5
d₁=20-14=6
d₂=20-16=4
Modus=Lₒ+[d₁/(d₁+d₂)] × p
=48,5+[6/(6+4)] × 5
=48,5 + [6/10] ×5
= 48,5 + [6/2]
= 51,5
Jadi, modus data pada tabel di atas adalah 51,5.
Soal 11
Perhatikan tabel data gaji per bulan sejumlah karyawan di Perusahaan Jaya Cemerlang berikut ini.
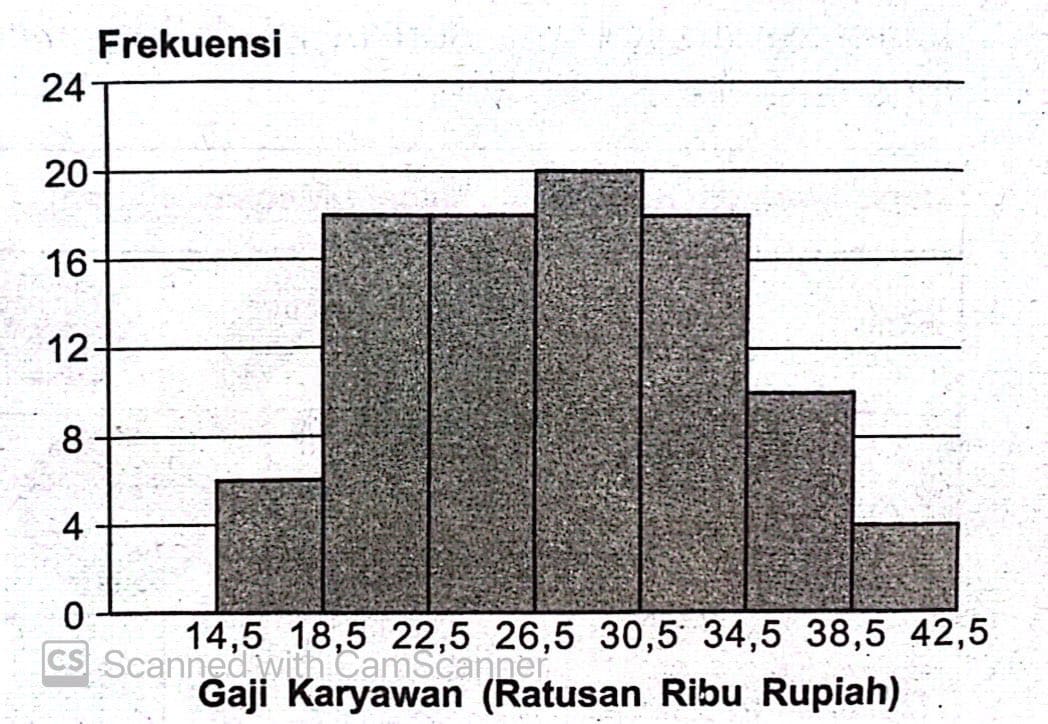
Median gaji karyawan adalah…
Pembahasan:
Jumlah data (n) = 6+18+18+20+16+10+4=92
Median:
Mₑ = nilai data ke-½(n+1)
= nilai data ke-½(92+1)
= nilai data ke-46,5
Perhatikan letak Mₑ atau nilai data ke-46,5 dalam gambar tabel berikut
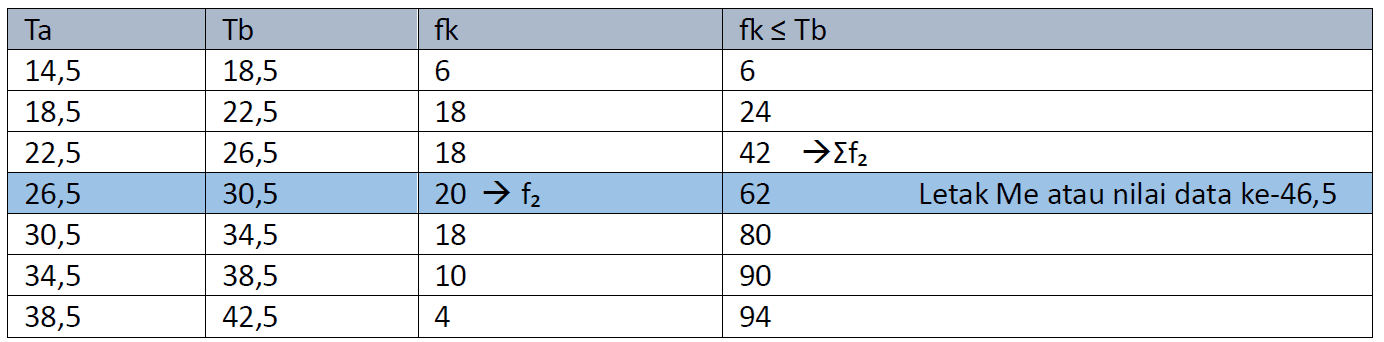
Dari tabel terlihat Mₑ terletak pada kelas interval yang memiliki tepi bawah Tb=26,5 dan tepi atas Ta=30,5 sehingga diperoleh:
p=30,5-26,5=4
L₂=26,5
f₂=20
Sf₂=42
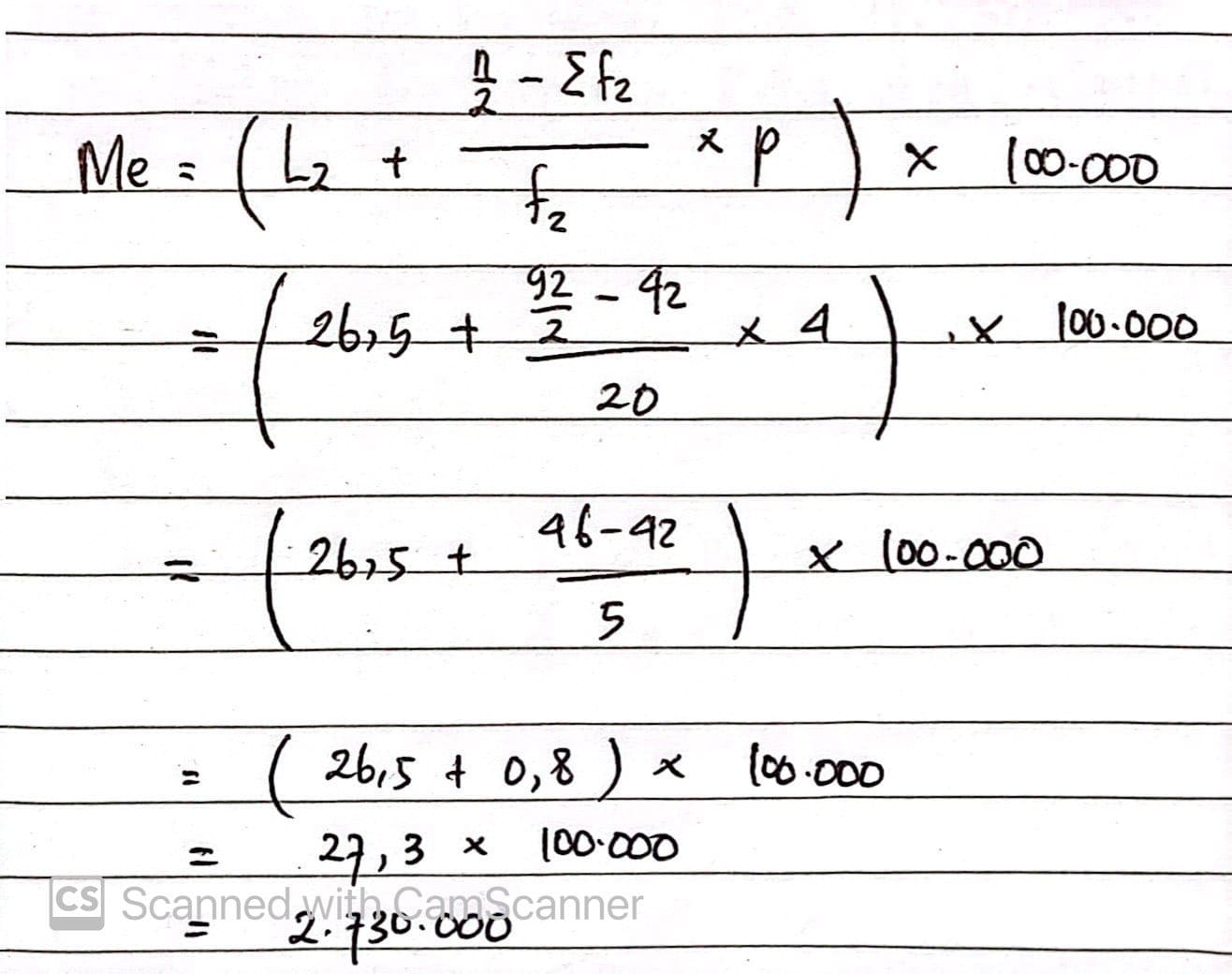
Jadi, median gaji karyawan adalah Rp 2.730.000
Soal 12
Hasil penimbangan berat badan 40 siswa sebagai berikut.
| Berat Badan (Kg) | Frekuensi |
| 34-38 | 2 |
| 39-43 | 14 |
| 44-48 | 8 |
| 49-53 | 10 |
| 54-63 | 6 |
Rata-rata berat badan siswa adalah…
Pembahasan:
Titik Tengah kelas interval adalah xi = ½(Bb + Ba)

Berdasarkan rumus rata-rata berat badan siswa= 1860/40 = 46,5
Jadi, rata-rata berat badan siswa adalah 46,5 kg.
Soal 13
Diberikan data seperti berikut ini:
7,3,2,10,6,8,5,4,1,9
Hitunglah kuartil pertama (Q₁) dan kuartil ketiga (Q₃).
Pembahasan:
Banyak data (n) = 10
Langkah pertama yang harus kita lakukan adalah menguturkan datanya.
1,2,3,4,5,6,7,8,9,10
Selanjutnya kita gunakan rumus untuk menghitung kuartil.
Q₁ = nilai data ke-1/4(n+1)
= nilai data ke-1/4(10+1)
= nilai data ke-1/4(11)
= nilai data ke-2,75
Karena berada di antara 2 dan 3 maka kita harus menghitung rata-rata dari angka yang berada di posisi 2 dan 3 tersebut yaitu (2+3)/2 = 2,5.
Q₃ = nilai data ke-3/4(n+1)
= nilai data ke-3/4(10+1)
= nilai data ke-3/4(11)
= nilai data ke-8,25
Karena berada di antara 8 dan 9 maka kita harus menghitung rata-rata dari angka yang berada di posisi 2 dan 3 tersebut yaitu (8+9)/2 = 8,5
Jadi, nilai.Q₁ =2,5 dan Q₃ =8,5.
Soal 14
Diketahui data berikut.
| Nilai | Frekuensi |
| 66-70 | 8 |
| 71-75 | 10 |
| 76-80 | 12 |
| 81-85 | 18 |
| 86-90 | 15 |
| 91-95 | 13 |
| 96-100 | 4 |
| Jumlah | 80 |
Kuartil atas data di atas adalah…
Pembahasan:
Banyak data (n) = 80
Kuartil atas (Q₃) = nilai data ke-¾ (n+1)
= nilai data ke-¾ (80+1)
= nilai data ke-60,75
Perhatikan letak nilai data ke-60,75 dalam tabel berikut:

Nilai data ke-60,75 terletak pada kelas interval 86-90
L₃ = 86- 0,5 = 85,5
ΣfQ₃ = 48
fQ₃ = 15
p=90-86+1=5
\(Q_{3}=L_{3}+\frac{\frac{3}{4}n-\sum f_{Q_{3}}}{f_{Q_{3}}}\times p\)
\(=85,5+\frac{\frac{3}{4}\times 80-48}{15}\times 5\)
\(=85,5+\frac{60-48}{3}\)
\(=85,5+\frac{12}{3}\)
\(=89,5\)
Jadi, kuartil atas data adalah 89,5.
Soal 15
Data berat badan siswa suatu sekolah sepak bola disajikan dalam tabel berikut.
| Berat Badan (Kg) | Frekuensi |
| 30-34 | 4 |
| 35-39 | 7 |
| 40-44 | 11 |
| 45-49 | 10 |
| 50-54 | 5 |
| 55-59 | 3 |
Nilai persentil ke-88 berat badan siswa adalah…
Pembahasan
Banyak data:
n = 4+7+11+10+5+3=40
Persentil ke-88:
P₈₈ = nilai data ke- 88/100 (n+1)
= nilai data ke-88/100 (40+1)
= nilai data ke-36,08
Perhatikan letak P₈₈ atai nilai data ke-36,08 dalam tabel frekuensi komulatif berikut.
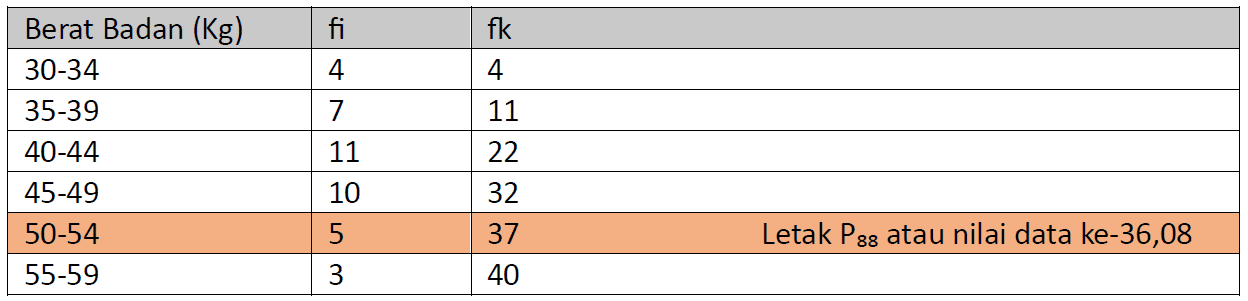
Nilai P₈₈ berada dalam kelas interval 50-54 sehingga diperoleh:
L₈₈ = 50-0,5=49,5
Σfp₈₈ = 32
fp₈₈ = 5
p = 54-50+1=5
\(P^{88}=L^{88}+\frac{\frac{88}{100}n-\sum f_{P_{88}}}{f_{_{88}}}\times p\)
\(=49,5+\frac{\frac{88}{100}\times 40-32}{5}\times 5\)
\(=49,5+35,3-32\)
\(=52,7\)
Jadi, nilai persentil ke-88 berat badan siswa adalah 52,7 kg.
Soal 16
Simpangan baku dari data 7,3,4,5,6,8 dan 2 adalah…
Pembahasan:
\(\overline{X}=\frac{7+3+4+5+6+8+2}{7}=\frac{35}{7}=5\)
\(\sum_{i=1}^{7}\left ( X_{i}-\overline{X} \right )^{2}\)
=(7-5)²+(3-5) ²+(4-5) ²+(5-5) ²+(6-5) ²+(8-5) ²+(2-5) ²
=2² + (-2)² + (-1)² + 0² + 1² + 3² + (-3)²
= 4+4+1+0+1+9+9
= 28
Simpangan baku:
\(S=\sqrt{\frac{1}{n}\sum_{i=1}^{7}\left ( Xi-\overline{X} \right )^{2}}\)
\(=\sqrt{\frac{1}{7}\times 28}=\sqrt{4}=2\)
Jadi, simpangan baku data adalah 2.
Soal 17
Perhatikan tabel data nilai ulangan suatu kelas berikut.
| Nilai | Frekuensi |
| 50-54 | 4 |
| 55-59 | 6 |
| 60-64 | 8 |
| 65-69 | 10 |
| 70-74 | 8 |
| 75-79 | 4 |
Nilai simpangan bakunya adalah…
Pembahasan:
Pada contoh simpangan baku ini, kita perlu mencari nilai rata-ratanya terlebih dahulu. Untuk mempermudah perhitungan, kita gunakan bantuan tabel, ya! Kamu juga boleh menghitung dengan bantuan kalkulator!
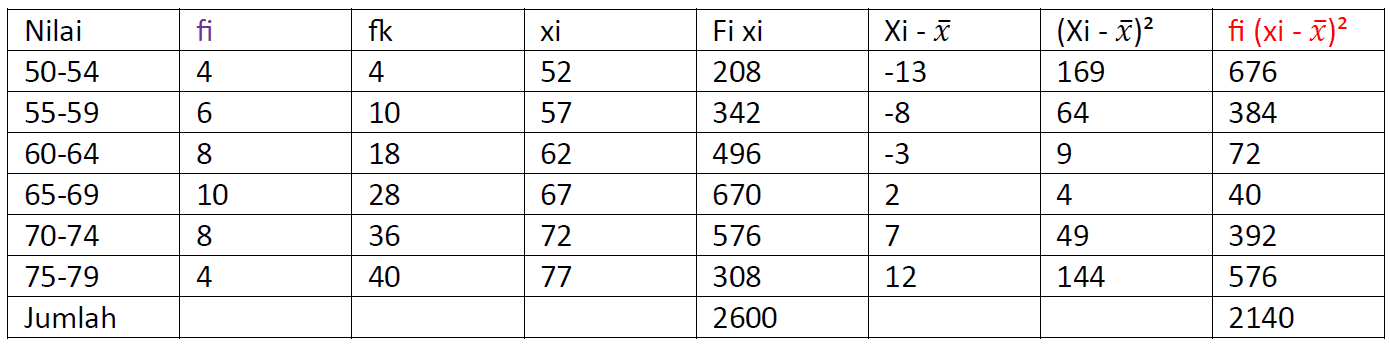
Berdasarkan tabel distribusi frekuensi di atas, dapat kita cari rata-ratanya dengan rumus berikut
\(S=\sqrt{S^{2}}=\sqrt{\frac{1}{\sum_{i=1}^{k}}\sum_{i=1}^{k}f_{i}\left( Xi-\overline{X} \right )^{2}}\)
\(=\sqrt{\frac{1}{40}\times 2140}=\sqrt{53,5}\)
Jadi, nilai simpangan bakunya adalah √53,5.
Soal 18
Kepada tiga orang siswa yaitu Andi, Tito dan Vian diberikan ulangan harian susulan mata Pelajaran matematika. Untuk dapat mencapai nilai KKM (Kriteria Ketuntasan Minimal), peluang Andi ⅘, peluang Tito ⅔ dan peluang Vian ¾. Peluang bahwa minimal dua di antara tiga siswa tersebut dapat mencapai nilai KKM adalah…
Pembahasan:
Peluang Andi mencapai KKM adalah P(A) = 4/5
Peluang Tito mencapai KKM adalah P(T) = 2/3
Peluang Vian mencapai KKM adalah P(V) = ¾
Kejadian Andi, Tito dan Vian mencapai nilai KKM merupakan kejadian-kejadian saling bebas.
Peluang Andi dan Tito memenuhi KKM, sedangkan Vian tidak memenuhi KKM:
P(A ꓵ T ꓵ Vᶜ) = P(A) × P(T) × P(Vᶜ)
= ⅘ × ⅔ × (1 – ¾)
= 8/15 × ⅟₄ =8/60
Peluang Andi dan Vian memenuhi KKM, sedangkan Tito tidak memenuhi KKM:
P(A ꓵ V ꓵ Tᶜ) = P(A) × P(V) × P(Tᶜ)
= ⅘ × ¾ × (1 – ⅔)
= 12/20 × ⅟3 =12/60
Peluang Tito dan Vian memenuhi KKM, sedangkan Andi tidak memenuhi KKM:
P(T ꓵ V ꓵ Aᶜ) = P(T) × P(V) × P(Aᶜ)
= ⅔ × ¾ × (1 – ⅘)
= 6/12 × ⅟5 =6/60
Peluang Andi, Tito dan Vian memenuhi KKM:
P(A ꓵ T ꓵ V) = P(A) × P(T) × P(V)
= ⅘ × ⅔ × ¾
= 24/60
Peluang minimal dua anak memenuhi KKM:
P = P(A ꓵ T ꓵ Vᶜ) + P(A ꓵ V ꓵ Tᶜ) + P(T ꓵ V ꓵ Aᶜ) + P(A ꓵ T ꓵ V)
= 8/60 + 12/60 + 6/60 + 24/60
= 50/60
= 5/6
Jadi, peluang minimal dua anak memenuhi KKM adalah 5/6.
Soal 19
Sebuah kotak berisi 5 bola biru, 3 bola putih dan 1 bola merah. Dari dalam kotak tersebut diambil satu bola dan tidak dikembalikan. Kemudian diambil satu bola lagi secara acak. Peluang terambil dua bola berwarna sama adalah…
Pembahasan:
Dalam kotak terdapat 9 bola terdiri atas 5 bola biru, 3 bola putih, dan 1 bola merah. Dari kotak tersebut diambil 2 bola satu-satu tanpa pengembalian. Terambil dua bola berwarna sama berarti terambil bola berwarna biru-biru atau putih-putih.
A₁ = Kejadian terambil bola biru pada pengambilan pertama
A₂ = Kejadian terambil bola biru pada pengambilan kedua
Peluang terambil bola biru pada pengambilan pertama dan kedua:
P(A₁ ꓵ A₂) = P(A₁) × P(A₂|A₁)
= 5/9 × (5-1)/(9-1)
= 5/9 × 4/8
= 20/72
B₁ = Kejadian terambil bola putih pada pengambilan pertama
B₂ = Kejadian terambil bola putih pada pengambilan kedua
Peluang terambil bola putih pada pengambilan pertama dan kedua:
P(B₁ ꓵ B₂) = P(B₁) × P(B₂|B₁)
= 3/9 × (3-1)/(9-1)
= 3/9 × 2/8
= 6/72
Peluang terambil dua bola berwarna biru-biru atau putih-putih:
P = P(A₁ ꓵ A₂) + P(B₁ ꓵ B₂)
= 20/72 + 6/72
= 26/72
= 13/36
Jadi, peluang terambil dua bola berwarna sama adalah 13/36.
Soal 20
Sebuah kotak berisi 4 bola merah dan 5 bola putih. Dari dalam kotak tersebut diambil dua bola secara acak. Peluang terambil dua bola merah adalah…
Pembahasan:
Dari dalam kotak berisi 4 + 5 bola diambil 2 bola sekaligus.
Banyak hasil yang mungkin:
n(S) = ₉C₂
=9!/(2! ×(9-2)!)=(9×8×7!)/(2×1×7!)=36
A=kejadian terambil 2 dari 4 bola merah
n(A)= ₄C₂
=4!/(2! ×(4-2)!)=(4×3×2!)/(2×1×2!)=6
Peluang A:
P(A) = n(A)/n(S) = 6/36 = 1/6
Jadi, peluang terambil dua bola merah adalah 1/6.
Demikian “20 Contoh Soal Matematika Kelas 10 Semester 2“. Semoga Bermanfaat.