Statistika SMP – Berikut ini saya akan memberikan soal statistika SMP yang Gengs pelajari pada Kelas 9 beserta pembahasan. Soal Matematika tentang statistika ini terdiri dari 21 soal. Bagi Gengs yang masih belum terlalu paham materi statistika SMP, silahkan Gengs membuka tautan berikut ini: Materi Statistika SMP Kelas 9 Lengkap
Soal 1
Seorang guru matematika akan meneliti hasil ulangan matematika untuk materi statistika kelas 9 SMP Makmur Jaya. Pada SMP tersebut khususnya kelas 9 terdapat 4 kelas. Penelitian dilakukan di kelas 9A dan 9B. Sampel dari kejadian tersebut adalah…
Jawab:
Dari soal tersebut, populasinya yaitu seluruh siswa kelas 9. Maka sampelnya yaitu siswa kelas 9A dan 9B. Sampel merupakan bagian dari populasi.
Soal 2
Departemen Kesehatan melakukan penelitian terhadap siswa SMP di DKI Jakarta yang menderita sakit gigi. Populasi yang baik untuk penelitian tersebut adalah … .
Jawab:
Populasi adalah kumpulan objek yang lengkap dan memiliki sifat sama yang digunakan sebagai dasar penarikan kesimpulan. Maka, populasinya adalah seluruh siswa SMP di DKI Jakarta.
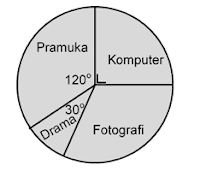
Perhatikan diagram lingkaran berikut ini!
Soal 3
Data tersebut merupakan data dari sekelompok siswa yang berjumlah 36 dengan berbagai kegiatan ekstrakurikuler yang diikuti. Banyaknya siswa yang mengikuti kegiatan pramuka dan Drama adalah…
Jawab:
Banyak anak yang mengikuti kegiatan ekstrakurukuler yaitu:
(120°/360°) x 36 = (1/3) x 36 = 12
Jadi, banyak anak yang mengikuti kegiatan ekstrakurikuler pramuka adalah 12 siswa.
Banyak anak yang mengikuti kegiatan ekstrakurikuler drama yaitu:
(30°/360°) x 36 = (1/12) x 36 = 3
Jadi, banyak anak yang mengikuti kegiatan ekstrakurikuler drama adalah 3 siswa.
Dengan demikian banyak siswa yang mengikuti kegiatan ekstrakurikuler pramuka dan drama yaitu 12+3=15 siswa
Soal 4
Dari data diagram lingkaran tersebut banyaknya siswa yang mengikuti kegiatan Komputer adalah…
Jawab:
Apabila kita perhatikan kembali diagram lingkaran di atas, pada kegiatan ekstrakurikuler komputer berbentuk segitiga siku-siku. Dimana segitiga siku-siku membentuk sudut 90°. Dengan demikian sama seperti soal 2, soal 3 pun akan kita peroleh dengan cara perhitungan soal 2.
Banyak anak yang mengikuti kegiatan ekstrakurikuler komputer yaitu:
(90°/360°) x 36 = (1/4) x 36 = 9 siswa
Soal 5
Dari data diagram lingkaran tersebut banyaknya siswa yang mengikuti kegiatan ekstrakulikuler fotografi adalah…
Jawab:
Karena pada soal sebelumnya telah kita peroleh banyaknya siswa yang mengikuti ektrakurikuler pramuka, drama dan computer maka dengan mudah kita akan peroleh siswa yang mengikuti ektrakurikuler fotografi.
Berikut penyelesaiannya:
36 – [12+3+9]=36-24 = 12 siswa
Bisa juga kita menghitung dengan berpatokan pada sudut.
Pada kegiatan ekstrakurikuler pramuka =120°
Pada kegiatan ekstrakurikuler drama = 30°
Pada kegiatan ekstrakurikuler komputer = 90°
Sisanya yaitu = 360° – [120°+30°+90°]=360° – 240° = 120°
Dengan demikian:
(120°/360°) x 36 = (1/3) x 36 = 12 siswa
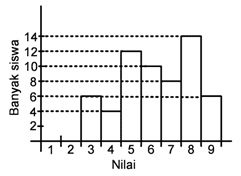
Data hasil ulangan matematika kelas 9 SMP Nusantara disajikan dalam bentuk histogram sebagai berikut ini.
Soal 6
Dari data yang ditampilkan dalam bentuk histogram, hasil ulangan tertinggi diperoleh berapa siswa…
Jawab:
Dari data histogram tersebut nilai tertinggi yaitu angka 9. Apabial kita lihat nilai dengan angka 9 dicapai oleh 6 siswa.
Diagram berikut untuk mengerjakan soal 7 dan soal 8.
Soal 7
Kenaikan angka kelahiran tertinggi terjadi pada tahun….
Jawab:
Mari jabarkan tingkat kenaikan tiap tahunnya.
Pada tahun 2010-2011 kenaikan angka kelahiran sebesar 50
Pada tahun 2011-2012 kenaikan angka kelahiran sebesar -100
Pada tahun 2012-2013 kenaikan angka kelahiran sebesar 150
Pada tahun 2013-2014 kenaikan angka kelahiran sebesar 100
Dengan demikian kenaikan angka kelahiran tertinggi terjadi pada tahun 2012-2013 yaitu sebanyak 150
Soal 8
Jumlah angka kelahiran sejak 2012 sampai 2014 adalah….
Jawab:
Pada tahun 2012-2013 kenaikan angka kelahiran sebesar 150
Pada tahun 2013-2014 kenaikan angka kelahiran sebesar 100
Dengan demikian, pada tahun 2012-2014 jumlah angka kelahiran sebesar 150+100=250
Soal 9
Diketahui data: 6,9,9,8,7,7,5,15,14,4. Nilai rata-ratanya adalah…
Jawab:
Karena pada soal yang ditanyakan adalah rata-rata, maka kita tidak perlu lagi mengurutkan data dari data yang terkecil.
Rata-rata = (6+9+9+8+7+7+5+15+14+4)/10 =84/10 = 8,4
Jadi, rata-ratanya adalah 8,4
Soal 10
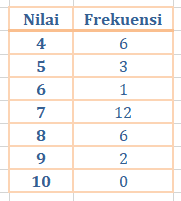
Tabel frekuensi berikut menunjukkan hasil ulangan matematika.
Banyak siswa yang mendapat nilai lebih dari 6 adalah….
Jawab:
Arti dari lebih dari 6 yaitu siswa yang mendapat nilai 7, 8, 9, 10
Dengan demikian,
Banyak siswa yang mendapat nilai lebih dari 6 yaitu: 12+6+2+0 = 20 siswa
Soal 11
Data nilai ulangan mata pelajaran Matematika sebagi berikut :
6, 7, 6, 4, 3, 9, 4, 5, 7, 3, 8, 6, 7, 7
Modus dari nilai di atas adalah ….
Jawab:
Modus adalah nilai yang frekuensinya paling banyak atau nilai data yang sering muncul.
Untuk menjawab soal ini alangkah baiknya jika kita mengurutkan dahulu data di atas. Seperti berikut.
3, 3, 4, 4, 5, 6, 6, 6, 7, 7, 7, 7, 8 ,9
Dengan demikian, dapat kita lihat bahwa angka 3 dan 4 muncul sebanyak 2 kali, angka 5, 8 dan 9 muncul sekali, angka 6 muncul 3 kali, angka 7 muncul sebanyak 4 kali. Maka modus dari data nilai ulangan mata pelajaran matematika tersebut adalah 7
Soal 12
Nilai ulangan Matematika suatu kelas tercatat sebagai berikut :
7, 7, 8, 4, 5, 7, 7, 5, 8, 5, 6, 7, 6, 9, 6, 6, 7, 9, 4
Median dari nilai tersebut di atas adalah … .
Mediannya adalah …
Jawab:
Median adalah nilai tengah setelah data diurutkan. Untuk mencari median ini, pertama-tama kita diharuskan untuk mengurutkan datanya terlebih dahulu.
Setelah diurutkan, datanya akan tampak sebagai berikut.
4, 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 8, 8, 9, 9
Selanjutnya kita hitung, berapa banyak data tersebut. Jika banyak data ganjil maka mediannya adalah nilai data yang terletak tepat di tengah-tengah. Jika banyak data genap maka mediannya adalah nilai rata-rata dari dua nilai data yang terletak di tengah.
Data tersebut terdapat 19 data. Karena banyak data ganjil maka mediannya adalah nilai data yang terletak tepat di tengah-tengah.
Kita bisa mengetahuinya dengan cara berikut
½ (n+1) = ½(19+1)=1/2(20)=10
Jadi mediannya yaitu data ke 10 yaitu 7.
Soal 13
Jika mean (rata-rata hitung) dari data 8, 10, 6, 7, 12, 5, 3, x adalah 8. Maka nilai x adalah …
Jawab:
Rumus untuk mencari rata-rata hitung yaitu
Rata-rata hitung = [data pertama + data kedua + … + data ke-n]/ n (banyaknya data)
Rumus ini pun yang akan kita gunakan untuk mencari jawaban dari soal 12
8 = [8+10+6+7+12+5+3+x]/8
8 = [51+x]/8
51+x = 64
x = 64 – 51 = 13
Jadi, nilai x adalah 13
Soal 14
Nilai ulangan bahasa Indonesia kelas 9A dinyatakan dalam tabel berikut.
Modus dari data tersebut adalah….
Jawab:
Jika soalnya sudah dalam tabel disertai frekuensinya, maka kita tidak perlu repot-repot menghitung banyak nilai yang muncul paling banyak. Kita cukup melihat nilai mana yang memiliki frekuensi terbesar.
Dengan demikian modus dari data tersebut adalah 8 karena muncul paling banyak yaitu sebanyak 13 kali.
Bagaimana jika yang ditanyakan adalah medianya.
Untuk mediannya, kita perlu tahu total dari frekuensi yaitu 36. Karena banyak data genap maka mediannya adalah nilai rata-rata dari dua nilai data yang terletak di tengah.
Dua nilai data yang terletak di tengah yaitu 36/2=18
Apabila dari kiri data ke-18 terletak di nilai 8
Apabila dari kanan data ke-18 terletak di nilai 8
Dengan demikian mediannya adalah 8
Soal 15
Dari data 3, 4, 3, 6, 5, 4, 4, 7, 6, 3 tersebut nilai kuartil bawah dan kuartil atas berturut-turut adalah….
Jawab:
Kuartil bawah disebut juga Q₁ dan kuartil atas disebut juga Q₃.
Untuk mencari Q₁ dan Q₃ akan kita gunakan rumus berikut:
Sebelum kita masuk ke rumusnya, mari kita urutkan datanya terlebih dahulu.
3, 3, 3, 4, 4, 4, 5, 6, 6, 7
Banyak data yaitu 10
Q₁= ¼ (n+1) = ¼ (10+1) = 11/4 =2,75 [antara 2 dan 3]
Karena berada diantara 2 dan 3 maka kita harus menghitung rata-rata dari angka yang berada di posisi 2 dan 3 tersebut yaitu (3+3)/2 = 3
Q₃ = ¾ (n+1) = ¾ (10+1) = 33/4 = 8,25 [antara 8 dan 9]
Karena berada diantara 8 dan 9 maka kita harus menghitung rata-rata dari angka yang berada di posisi 8 dan 9 tersebut yaitu (6+6)/2 = 6
Soal 16
Nilai rata-rata IPA dari 8 anak adalah 6,3. Apabila ditambah nilai satu anak baru, maka rata-ratanya menjadi 6,1. Nilai anak yang baru adalah …
Jawab:
Rumus yang akan kita gunakan yaitu:
Rata-rata = total seluruh nilai / total siswa
Pertama akan kita hitung untuk 8 siswa.
Rata-rata = total seluruh nilai / total siswa
6,3 = total seluruh nilai / 8
Total seluruh nilai = 6,3 (8) = 50,4
Selanjutnya kita hitung untuk 9 siswa [setelah ditambah dengan nilai anak baru]
Rata-rata = total seluruh nilai / total siswa
6,1 = total seluruh nilai / 9
Total seluruh nilai = 6,1 (9) = 54,9
Jadi, nilai anak baru yaitu 54,9 – 50,4 = 4,5
Soal 17
Sebanyak 20 siswa SMPN 1 Banten ditimbang berat badannya (dalam) kg. Diperoleh data sebagai berikut.
50,45,43,49,50,52,41,47,45,46
48,46,48,51,53,47,49,52,58,47
Selisih kuartil atas dan kuartil bawah adalah …
Jawab:
Langkah 1: Urutkan dari data terkecil sebagai berikut.
41,43,45,45,46,46,47,47,47,48,
48,49,49,50,50,51,52,52,53,58
Langkah 2: Menghitung kuartil dengan rumus
Q₁ = ¼ (n+1) = ¼ (20+1) = ¼ (21) = 5,25 [antara 5 dan 6]
Karena berada diantara 5 dan 6 maka kita harus menghitung rata-rata dari angka yang berada di posisi 5 dan 6 tersebut yaitu (46+46)/2 = 46
Q₃ = ¾ (n+1) = ¾ (20+1) = ¾ (21) = 15,75 [antara 15 dan 16]
Karena berada diantara 15 dan 16 maka kita harus menghitung rata-rata dari angka yang berada di posisi 15 dan 16 tersebut yaitu (50+51)/2 = 50,5
Dengan demikian, selisih kuartil atas dan kuartil bawah adalah 50,5 – 46 = 4,5
Soal 18
Nilai rata-rata ulangan matematika dari 30 siswa adalah 5,8. Jika nilai itu digabungkan dengan nilai dari 8 siswa lagi, maka nilai rata-ratanya menjadi 6,0. Nilai rata-rata 8 siswa tersebut adalah …
Jawab:
Rumus yang akan kita gunakan yaitu:
Rata-rata = total seluruh nilai / total siswa
Pertama akan kita hitung untuk 8 siswa.
Rata-rata = total seluruh nilai / total siswa
5,8 = total seluruh nilai / 30
Total seluruh nilai = 5,8 (30) = 174
Selanjutnya kita hitung untuk 38 siswa [setelah ditambah dengan nilai dari 8 siswa]
Rata-rata = total seluruh nilai / total siswa
6,0 = total seluruh nilai / 38
Total seluruh nilai = 6,0 (38) = 228
Langkah terakhir kita hitung nilai rata-rata untuk 8 siswa.
Rata-rata = total nilai / total siswa
= (228-174)/ 8
= 54/8 = 6,75
Jadi, nilai rata-rata 8 siswa tersebut adalah 6,75
Soal 19
Data nilai ulangan mata pelajaran Matematika sebagi berikut :
6, 7, 6, 4, 3, 9, 4, 5, 7, 3, 8, 6, 7, 7
Modus dari nilai di atas adalah ….
Jawab
Modus adalah nilai yang frekuensinya paling banyak atau nilai data yang sering muncul.
Data tersebut apabila
3, 4 muncul sebanyak 2
5, 8, 9 muncul sebanyak 1
6 muncul sebanyak 3
7 muncul sebanyak 4
Jadi, data yang muncul paling banyak adalah 7 yaitu sebanyak 4 kali.
Soal 20
Nilai ulangan Matematika suatu kelas tercatat sebagai berikut :
7, 7, 8, 4, 5, 7, 7, 5, 8, 5, 6, 7, 6, 9, 6, 6, 7, 9
Mean dari nilai tersebut di atas adalah … .
Jawab:
Mean = Total nilai / banyaknya data
= (7+7+8+4+5+7+7+5+8+5+6+7+6+9+6+6+7+9)/18
= 6,6
Soal 21
Perhatikan tabel berikut ini.
Tabel tersebut menunjukkan data nilai ujian matematika sekelompok siswa. Nilai rata-rata dari data tersebut adalah….
Jawab:
Maka, nilai rata-rata dari data tersebut adalah 6,05
Baca Juga: Ukuran Pemusatan Data (Soal dan Jawaban)
Dengan soal statistika SMP kelas 9 ini, saya harap bisa membantu Gengs sekalian khususnya bagi Gengs yang berada di kelas 9.
7 komentar di “21 Soal Statistika SMP Kelas 9 Plus Jawaban”
Tinggalkan Balasan
Anda harus masuk untuk berkomentar.

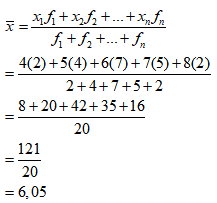
Hi there,
We run an Instagram growth service, which increases your number of followers both safely and practically.
– We guarantee to gain you 400-1000+ followers per month.
– People follow you because they are interested in you, increasing likes, comments and interaction.
– All actions are made manually by our team. We do not use any ‘bots’.
The price is just $60 (USD) per month, and we can start immediately.
If you’d like to see some of our previous work, let me know, and we can discuss it further.
Kind Regards,
Megan
Hi there,
We run an Instagram growth service, which increases your number of followers both safely and practically.
– We guarantee to gain you 400-1000+ followers per month.
– People follow you because they are interested in you, increasing likes, comments and interaction.
– All actions are made manually by our team. We do not use any ‘bots’.
The price is just $60 (USD) per month, and we can start immediately.
If you’d like to see some of our previous work, let me know, and we can discuss it further.
Kind Regards,
Libby
Hi there,
We run an Instagram growth service, which increases your number of followers safely and practically.
We aim to gain you 400-1200+ real human followers per month, with all actions safe as they are made manually (no bots).
The price is just $60 (USD) per month, and we can start immediately.
Let me know if you wish to see some of our previous work.
Kind Regards,
Megan
Hi,
I am getting in touch to present a valuable guest post offer for your website which will help boosting your traffic as well as build links. You will just have to publish it on your site with my backlink.
Interested in working together on this? If yes, I’ll send you the topics.
Looking forward to hearing from you.
Best,
Wendy Gill
Hi,
I intend to contribute a guest post to your website that will help you get good traffic as well as interest your readers.
Shall I send you the topics then?
Best,
Sophia
Hi,
I intend to contribute a guest post to your website that will help you get good traffic as well as interest your readers.
Shall I send you the topics then?
Best,
John