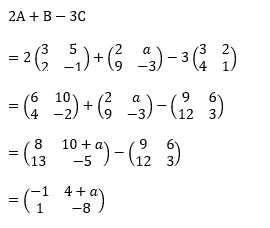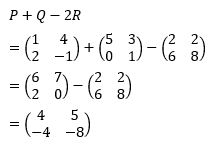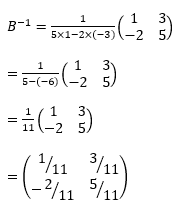Dalam ilmu matematika matriks adalah susunan bilangan, simbol, atau ekspresi yang disusun dalam baris dan kolom sehingga membentuk suatu bangun persegi. Determinan matriks didefinisikan sebagai selisih antara perkalian elemen-elemen pada diagonal utama dengan perkalian elemen-elemen pada diagonal sekunder. Determinan matriks hanya dapat ditentukan pada matriks persegi (nxn). Determinan dari matriks A dapat dituliskan det(A) atau |A|.
Berikut ini, 10 soal dan pembahasan tentang determinan matriks.
Soal 1
Tentukan determinan dari matriks \(A=\left( \begin{matrix}
-2 &-4 \\
8 &16
\end{matrix} \right)\)
-2 &-4 \\
8 &16
\end{matrix} \right)\)
Jawaban:
Rumus yang kita akan gunakan untuk mencari nilai determinan yaitu:
Misalkan diketahui matriks \(B=\left ( \begin{matrix} a &b \\ c &d \end{matrix} \right )\), maka det B = ad – bc
Dengan demikian det (A)= -2(16) – 8(-4) = -32 – (-32) = -32 + 32 = 0
Soal 2
Jika nilai determinan dari matriks \(\left ( \begin{matrix} 2a &3 \\ -2 &2 \end{matrix} \right )\) adalah -6, nilai a adalah…
Jawaban:
Kita misalkan matrik diatas dengan matriks A.
Karena nilai determinan A adalah -6 maka:
2a(2) – (-2)(3) = -6
4a – (-6) = -6
4a + 6 = -6
4a = -6-6
4a = -12
a= -3
Dengan demikian nilai a adalah -3.
Soal 3
Diketahui determinan \(\left ( \begin{matrix} 5x &x \\ 3x &3 \end{matrix} \right )\) adalah 18, nilai x yang memenuhi adalah…
Jawaban:
Kita misalkan matrik diatas dengan matriks A.
Karena nilai det (A) adalah 18 maka:
5x(3) – (3x)(x) = 18
15x – (3x²) = 18
-3x² + 15x – 18 = 0 (dibagi dengan -3)
x² – 5x – 6 = 0
(x+1)(x-6) = 0
x+1 =0 maka x=-1
x-6=0 maka x=6
Dengan demikian nilai x yang memenuhi adalah -1 dan 6.
Soal 4
Tentukan determinan dari matrik \(A=\left ( \begin{matrix} 3 &5 &1 \\ 2 &3 &1 \\ 1 &2 &2 \end{matrix} \right )\).
Jawaban:
Rumus yang kita akan gunakan untuk mencari nilai determinan yaitu:
Misalkan diketahui matriks \(B=\left ( \begin{matrix} a₁ &a₂ &a₃ \\ b₁ &b₂ &b₃ \\ c₁ &c₂ &c₃ \end{matrix} \right )\), maka det B = (a₁b₂c₃ + a₂b₃c₁ + a₃b₁c₂) – (a₃b₂c₁ + a₁b₃c₂ + a₂b₁c₃).
Dengan demikian,
det (A)= (3x3x2 + 5x1x1 + 1x2x2) – (1x3x1 + 3x1x2 + 5x2x2) = (18+5+4)-(3+6+20) =27 – 29 = -2.
Soal 5
Tentukan determinan dari matrik \(A=\left ( \begin{matrix} -4 &0 &3 \\ 1 &7 &4 \\ 2 &5 &-1 \end{matrix} \right )\).
Jawaban:
Rumus yang kita akan gunakan sama seperti soal sebelumnya yaitu = (a₁b₂c₃ + a₂b₃c₁ + a₃b₁c₂) – (a₃b₂c₁ + a₁b₃c₂ + a₂b₁c₃).
Dengan demikian,
det (A) = (-4x7x-1 + 0x4x2 + 3x1x5) – (3x7x2 + -4x4x5 + 0x1x-1)
= (28+0+15)-(42+-80+0)
= 43 –(-38) = 81
Soal 6
Jika \(A=\left ( \begin{matrix} 3 &5 \\ 2 &-1 \end{matrix} \right )\), \(B=\left ( \begin{matrix} 2 &a \\ 9 &-3 \end{matrix} \right )\) dan \(C=\left (\begin{matrix} 3 &2 \\ 4 &1 \end{matrix} \right )\). Jika determinan matriks 2A+B-3C adalah 1, maka nilai a adalah….
Jawaban:
Karena det (2A+B-3C) = 1 maka:
det (2A+B-3C) = 1
(-1)(-8) – (1)(4+a) = 1
8-4-a = 1
4-a=1
a=3
Soal 7
Diketahui \(P=\left ( \begin{matrix} 1 &4 \\ 2 &-1 \end{matrix} \right )\),\(Q=\left ( \begin{matrix} 5 &3 \\ 0 &1 \end{matrix} \right )\) dan \(R=\left ( \begin{matrix} 1 &1 \\ 3 &4 \end{matrix} \right )\). Determinan matriks (P+Q-2R) adalah…
Jawaban:
Langkah awal mari kita hitung 2R.
\[R=\left ( \begin{matrix} 1 &1 \\ 3 &4 \end{matrix} \right )\]
\[2R=2\left ( \begin{matrix} 1 &1 \\ 3 &4 \end{matrix} \right )=\left ( \begin{matrix} 2 &2 \\ 6 &8 \end{matrix} \right )\]
Langkah kedua akan kita hitung P+Q-2R.
Langkah terakhir akan kita cari determinan dari P+Q-2R
det (P+Q-2R)= 4(-8) – (-4)(5) = -32 – (-20) = -32 +20 = -12
Dengan demkian nilai dari determinan dari matriks P+Q-2R adalah -12.
Soal 8
Diketahui matriks \(P=\left ( \begin{matrix} -2 &1 \\ 6 &4 \end{matrix} \right )\). Tentukan determinan matriks S jika S=-4P.
Jawaban:
Sebelum mencari nilai determinannya, kita cari terlebih dahulu S=-4P
\(P=\left ( \begin{matrix} -2 &1 \\ 6 &4 \end{matrix} \right )\)
S=-4P
\(S=-4\left ( \begin{matrix} -2 &1 \\ 6 &4 \end{matrix} \right )=\left ( \begin{matrix} 8 &-4 \\ -24 &-16 \end{matrix} \right )\)
Setelah mendapatkan nilai S, sekarang kita akan memcari nilai determinan dari S.
det (S) = -16(8) – (-24)(-4) = -128 – 96 = -224
Dengan demikian nilai determinan S adalah -224.
Soal 9
Diketahui matriks \(A=\left ( \begin{matrix} 4 &2 \\ 3 &-4 \end{matrix} \right )\) dan \(B=\left ( \begin{matrix} 5 &-3 \\ 2 &1 \end{matrix} \right )\). Jika AC=B dan C¯¹ adalah invers matriks C, maka determinan dari matriks C¯¹ adalah…
Jawaban:
Sebelum mencari nilai determinan dari matriks C¯¹, kita cari dahulu invers dari matriks C.
Karena AC= B maka C¯¹ = B¯¹A
Matriks A telah diketahui pada soal sedangkan B¯¹ belum diketahui. Oleh karena itu akan kita cari B¯¹ dari matriks B yang telah diketahui pada soal.
\[B=\left ( \begin{matrix} 5 &-3 \\ 2 &1 \end{matrix} \right )\]
Rumus yang akan kita gunakan untuk mencari invers dari suatu matriks yaitu:
Misalkan matriks \(P=\left ( \begin{matrix} a &b \\ c &d \end{matrix} \right )\), maka invers dari matriks P adalah:
\[P^{-1}=\frac{1}{ad-bc}\left ( \begin{matrix} d &-b \\ -c &a \end{matrix} \right )\]
Dengan demikian
Karena B¯¹ sudah ditemukan selanjutnya akan kita cari C¯¹ = B¯¹A
Dengan demikian kita dapat mencari nilai determinan dari matriks C¯¹.
\(det(C^{-1}) \)= [(13/11) ×(-24/11)] – [(7/11) × (-10/11) ]
= (-312/121) – (-70/121)
= -241/121
= -2
Pelajari Juga: Contoh Soal Matriks Invers dan Pembahasan
Soal 10
Jika \(P=\left ( \begin{matrix} 2 &0 \\ -1 &1 \end{matrix} \right )\) dan \(Q=\left ( \begin{matrix} 3 &-2 \\ -1 &4 \end{matrix} \right )\). Jika R=3P-2Q, determinan R adalah…
Jawaban:
R=3P-2Q
\(=3\left ( \begin{matrix} 2 &0 \\ -1 &1 \end{matrix} \right )-2\left ( \begin{matrix} 3 &-2 \\ -1 &4 \end{matrix} \right )\)
\(=\left ( \begin{matrix} 6 &0 \\ -3 &3 \end{matrix} \right )-\left ( \begin{matrix} 6 &-4 \\ -2 &8 \end{matrix} \right )\)
\(=\left ( \begin{matrix} 0 &4 \\ -1 &-5 \end{matrix} \right )\)
Dengan demikian,
det (R) = (0)(-5) – (-1)(4) = 0-(-4) = 4
Pelajari Juga: