Berikut ini penjelasan singkat tentang cara menentukan eksterm global dan ekstrem lokal disertai contoh dan pembahasannya.
Definisi Nilai Ekstrem Global dan Ekstrem Lokal:
Fungsi f memiliki maksimum lokal di \(D_{f}\) jika f(c) ≥ f(x), ∀x anggota selang tertutup yang memuat c. Fungsi f memiliki minimum lokal di \(D_{f}\) jika f(c) ≤f(x), ∀x anggota selang terbuka yang memuat c.
Misalkan fungsi f terdefinisikan pada daerah asal D, maka:
Fungsi f memiliki maksimum global di c∈D jika f(c)≥ f(x),∀x∈D. f(c) disebut nilai maksimum f pada D.
Fungsi f memiliki minimum global di c∈D jika f(c)≤f(x), ∀x ∈ D. f(c) disebut nilai maksimum f pada D.
ILUSTRASI

Teorema:
Jika f kontinu pada selang tertutup [a,b], maka f memiliki minimum mutlak m=f(x₁) dan maksimum mutlak m=f(x₂), x₁, x₂ ∈[a,b].
Artinya:
Jika f kontinu pada [a,b], maka f memiliki maksimum mutlak dan minimum mutlak.
Jika f tak kontinu pada [a,b], maka tidak ada kesimpulan apakah f memiliki minimum mutlak atau maksimum mutlak.
Cara Menentukan Ekstrem Global dan Ekstrem Lokal
Ekstrem Global
Misalkan f terdefinisikan pada [a,b] maka:
1. Tetapkan bilangan-bilangan kritis pada (a,b)
Bilangan kritis adalah bilangan c di (a,b) dengan f ‘(c) = 0 atau f ‘(c) tidak ada
2. Evaluasi f pada bilangan kritis dan titik-titik ujung a dan b
Nilai terbesar –> maksimum global
Nilai terkecil –> minimum global
Ekstrem Lokal
1. Cari bilangan kritis c
2. Periksa tanda nilai f ‘ pada selang antara bilangan kritis atau ujung selang
3. Jika f ‘ berbeda tanda [ ++++ —–] maka f(c) maksimum lokal
Jika f ‘ berbeda tanda [—- ++++] maka f(c) minimum lokal
Jika f ‘ tidak berbeda tanda maka f tidak memiliki ekstrem lokal.
CONTOH
\(f(x)=\frac{x}{x+1};xin [1,2]\)
Pertama-tama. tentukan bilangan kritisnya:
f ‘(x) = 0
\(\Leftrightarrow \frac{x+1-x}{(x+1)^{2}}=0\)
\(\frac{1}{(x+1)^{2}}=0\)
maka tidak ada x yang memenuhi.
f ‘(x) tidak ada <–> x + 1 = 0 <–> x = -1 bukan anggota [1,2]
maka f tidak mempunyai bilangan kritis
f(1) = 1/2 ………….. f(1) minimum global
f(2) = 2/3 ………….. f(2) maksimum global
CATATAN
Misalkan f fungsi kontinu dan f ‘(x) dan f ”(x) ada
Turunan pertama: untuk mengetahui naik/turun fungsi f di suatu selang
a. f ‘(x) > 0 pada suatu selang maka f naik pada selang tersebut.
b. f ‘(x) < 0 pada suatu selang maka f turun pada selang tersebut.
Turunan kedua: untuk mengetahui kecekungan fungsi f di suatu selang terbuka I.
a. f ”(x) > 0 , Untuk setiap x anggota I maka f cekung ke atas pada I
b. f ”(x) < 0 , Untuk setiap x anggota I maka f cekung ke bawah pada I
Uji turunan kedua pada ektrem lokal:
a. f ‘(c) = 0, f ”(c) > 0 maka f(c) minimum lokal
b. f ‘(c) = 0, f ”(c) < 0 maka f(c) maksimum lokal
c. f ‘(c) = 0, f ”(c) = 0 maka uji turunan kedua gagal
Misalkan f kontinu pada $cin I(a,b)$ dan f ”(c) = 0 atau f ”(c) tidak ada
Jika ++++++ – – – – – (f ”) maka (c , f(c)) adalah titik belok fungsi f.
CONTOH
Tentukan selang naik/turun, ekstrem lokal, selang kecekungan dan titik belok dari
f(x)=2x³+9x²-10
Tentukan turunan pertama
f'(x)=6x²-18x → f'(x)=0
→ f'(x)=6x²-18x
6x (x + 3) = 0
x = 0 atau x = -3
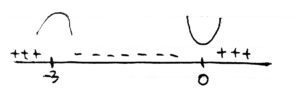
dari gambar di atas dapat ditentukan bahwa:
f naik pada (min tak hingga, -3) dan (0, tak hingga)
f turun pada (-3,0)
saat x = -3, f(-3) = 17 maka maksimum lokal
saat x = 0, f(0) = -10 maka minimum lokal
Tentukan turunan kedua
f ”(x) = 12x + 18
f ”(x) = 0
12x + 18 = 0
x = – 3/2
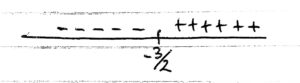
f cekung ke atas pada (-3/2 , takhingga)
f cekung ke bawah pada (min takhingga , -3/2)
Sehingga grafik fungsi f sebagai berikut:
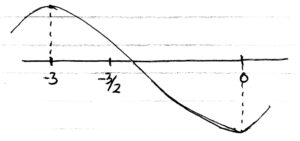
Oke dehh Gengs, sampai di sini dulu tentang Terapan Turunan – Cara Menentukan Ekstrem Global dan Ekstrem Lokal.
Bagi Gengs yang mau bertanya atau kritik, sokk ditulis di kolom komentar. Semoga Bermanfaat.
2 komentar di “Cara Menentukan Ekstrem Global dan Lokal”
Tinggalkan Balasan
Anda harus masuk untuk berkomentar.
alhamdulillah , sangat membantu sekali ~
terimakasih sender 🙂
Terima kasih juga telah berkomentar