Hiii Gengs… Apa kabar? Semoga sehat selalu. Pada kesempatan yang indah ini, saya akan berbagi artiket mengenai “Cara Konversi Bilangan Biner ke Desimal Lengkap dengan Contoh. Bagi Geng yang belum paham tentang “Cara Konversi Bilangan Biner ke Desimal”, Gengs dapat ikuti artikel ini hingga selesai.
Untuk mengkonversi bilangan biner ke bilangan desimal, Gengs dapat menggunakan 2 cara yaitu menggunakan notasi posisi atau menggunakan mengali dua. Pada artikel ini, untuk masing-masing metodenya akan diberikan contoh pengerjaannya.
Berikut ini adalah contoh pengerjaannya.
MENGGUNAKAN NOTASI POSISI
SOAL 1: Ubalah bilangan biner berikut \(10011011_2\) kedalam bilangan desimal.
Tuliskan angka biner dan daftar kuadrat 2 dari kanan ke kiri.
Misalnya pada soal di atas kita ingin mengubah angka biner \(10011011_2\) menjadi desimal.
Pertama. Tuliskan: \(10011011_2\)
Kemudian, tuliskan kuadrat 2 dari kanan ke kiri. Mulailah dari \(2^0\), yaitu 1. Naikkan pangkatnya satu per satu.

*Hentikan jika jumlah angka yang ada di daftar sama dengan banyaknya digit angka biner. Seperti pada contoh angka diatas, 10011011, memiliki 8 digit, jadi daftarnya memiliki 8 angka.
Tuliskan digit angka biner di bawah daftar kuadrat dua.
Tuliskan angka 10011011 di bawah angka 128, 64, 32, 16, 8, 4, 2, dan 1 sehingga setiap digit biner memiliki kuadrat angka duanya masing-masing.
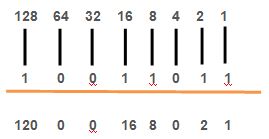
128 64 32 16 8 4 2 1
1 0 0 1 1 0 1 1
*Angka 1 di kanan angka biner sejajar dengan angka 1 dalam daftar kuadrat 2 dan selanjutnya. Untuk menuliskan bilangan binernya, Gengs bebas memilih apakah akan dituliskan dibawah daftar kuadrat ataukah akan dituliskan diatas daftar kuadrat yang telah diperoleh sebelumnya.
Hubungkan digit dari angka biner dengan daftar kuadrat dua.
Buatlah garis untuk menghubungkan setiap digit angka biner dengan kuadrat dua. Hal ini akan membantu Gengs dalam membayangkan hubungan antara kedua kumpulan angka tersebut.
Tuliskan nilai akhir setiap kuadrat dua.
Sisirlah setiap digit angka biner. Jika digitnya adalah 1, tulislah kuadrat dua pasangannya di bawah angka 1 tersebut. Jika digitnya adalah 0, tulislah 0 di bawah angka 0.
Catatan:
Karena 1 berpasangan dengan 1, hasilnya 1
Karena 2 berpasangan dengan 1, hasilnya 2
Karena 4 berpasangan dengan 0, hasilnya 0
Karena 8 berpasangan dengan 1, hasilnya 8
karena 16 berpasangan dengan 1, hasilnya 16
Karena 32 berpasangan dengan 0, hasilnya 0
Karena 64 berpasangan dengan 0, hasilnya 0
Karena 128 berpasangan dengan 1, hasilnya 128.
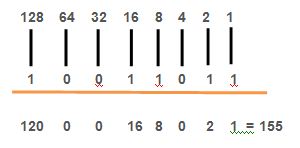
Tambahkan nilai akhirnya.
Selanjutnya adalah, tambahkan semua angka yang tertulis di bawah digit angka biner.
Tulislah jawaban akhir dengan subskrip basisnya.
Sekarang, Anda harus menulis \(155_10\), untuk menunjukkan bahwa angka itu adalah desimal, yang memiliki kelipatan 10.
SOAL 2: Ubalah bilangan biner berikut 10110012 kedalam bilangan desimal.
Tuliskan angka biner dan daftar kuadrat 2 dari kanan ke kiri.
Berdasarkan soal di atas, kita ingin mengubah angka biner \(1011001_2\) menjadi desimal.
Pertama. Tuliskan: \(1011001_2\)
Kemudian, tuliskan kuadrat 2 dari kanan ke kiri. Mulailah dari \(2^0\), yaitu 1. Kenaikan kuadrat satu per satu.

*Hentikan jika jumlah angka yang ada di daftar sama dengan banyaknya digit angka biner. Seperti pada contoh angka diatas, 1011001, memiliki 7 digit, jadi daftarnya memiliki 7 angka.
Tuliskan digit angka biner di bawah daftar kuadrat dua.
Tuliskan angka 1011001 di bawah angka 64, 32, 16, 8, 4, 2, dan 1 sehingga setiap digit biner memiliki kuadrat angka duanya masing-masing.
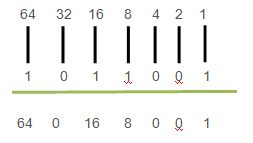
64 32 16 8 4 2 1
1 0 1 1 0 0 1
Hubungkan digit dari angka biner dengan daftar kuadrat dua.
Buatlah garis untuk menghubungkan setiap digit angka biner dengan kuadrat dua. Hal ini akan membantu Gengs dalam membayangkan hubungan antara kedua kumpulan angka tersebut.
Tuliskan nilai akhir setiap kuadrat dua.
Sisirlah setiap digit angka biner. Jika digitnya adalah 1, tulislah kuadrat dua pasangannya di bawah angka 1 tersebut. Jika digitnya adalah 0, tulislah 0 di bawah angka 0.
Catatan:
Karena 1 berpasangan dengan 1, hasilnya 1
Karena 2 berpasangan dengan 0, hasilnya 0
Karena 4 berpasangan dengan 0, hasilnya 0
Karena 8 berpasangan dengan 1, hasilnya 8
karena 16 berpasangan dengan 1, hasilnya 16
Karena 32 berpasangan dengan 0, hasilnya 0
Karena 64 berpasangan dengan 1, hasilnya 64.
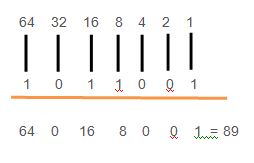
Tambahkan nilai akhirnya
Selanjutnya adalah, tambahkan semua angka yang tertulis di bawah digit angka biner.
Tulislah jawaban Anda dengan subskrip basisnya.
Sekarang, Anda harus menulis \(89_10\), untuk menunjukkan bahwa angka itu adalah desimal, yang memiliki kelipatan 10.
MENGGUNAKAN PENGALI DUA (Cara ini tidak menggunakan kuadrat)
SOAL 1: Ubalah bilangan biner berikut 100110112 kedalam bilangan desimal.
Tuliskan angka binernya.
Hal pertama yang perlu Gengs lakukan adalah menuliskan angka biner yang akan diubah menggunakan cara pengalian dua.
Mulailah dari kiri, kalikan total penjumlahan sebelumnya dengan dua dan tambahkan digitnya.
Karena Gengs menggunakan angka biner \(1011001_2\), digit pertama dari kiri adalah 1.

*Total penjumlahan sebelumnya adalah 0 karena belum ada perhitungan sebelumnya. Gengs harus mengalikan dua total penjumlahan dan tambahkan 1.
Kalikan total penjumlahan sebelumnya dengan basis kemudian tambahkan digit selanjutnya.
Total penjumlahan sebelumnya adalah 1 dikalikan dengan basis yaitu 2 dan tambahkan 0 (digit setelah 1)
Lakukan langkah di atas hingga semua digitnya berhasil dihitung.
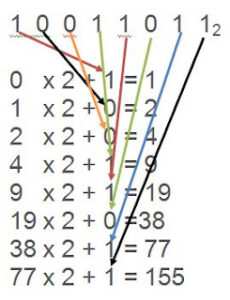
Tuliskan jawabannya dengan subskrip basisnya.
Tuliskan jawaban akhir \(155_10\) untuk menunjukkan angka desimal yang memiliki basis 10.
Gunakan cara ini untuk mengubah basis berapapun ke bentuk desimal.
Pengalian dua digunakan karena angka yang diberikan berbasis 2. Jika angka yang diberikan memiliki basis yang berbeda, gantilah 2 pada cara ini dengan basis angka tersebut. Misalnya, jika angka yang diberikan berbasis 80, gantilah x 2 dengan x 80.
SOAL 2: Ubalah bilangan biner berikut \(1011001_2\) ke dalam bilangan desimal.
Tuliskan angka binernya.
Hal pertama yang perlu Gengs lakukan adalah menuliskan angka biner yang akan Anda ubah menggunakan cara pengalian dua.
Misalkan seperti pada soal nomor 2, Gengs akan mengubah angka biner \(1011001_2\).
Mulailah dari kiri, kalikan dua total penjumlahan sebelumnya dan tambahkan digitnya.
Karena angka binernya adalah 10110012, maka digit pertama dari kiri adalah 1.

*Total penjumlahan sebelumnya adalah 0 karena belum ada perhitungan sebelumnya. Gengs harus mengalikan dua total penjumlahan dan tambahkan 1.
Kalikan total penjumlahan sebelumnya dengan basis kemudian tambahkan digit selanjutnya.
Total penjumlahan sebelumnya adalah 1 dikalikan dengan basis yaitu 2 dan tambahkan 0 (digit setelah 1)
Lakukan langkah di atas hingga semua digitnya berhasil dihitung.

Tuliskan jawabannya dengan subskrip basisnya.
Tuliskan jawaban akhir \(89_10\) untuk menunjukkan angka desimal yang memiliki basis 10.
Demikian Cara Konversi Bilangan Biner ke Desimal Disertai Contoh.
Pelajari Juga:
Semoga Bermanfaat.
Satu komentar di “Cara Konversi Bilangan Biner ke Desimal”
Tinggalkan Balasan
Anda harus masuk untuk berkomentar.
Saved as a favorite, I love your site!