Bangun ruang dan statistika merupakan dua materi yang dipelajari di jenjang SD kelas 6 semester 2. Pada kesempatan ini saya akan memberika 10 soal matematika yang berkaitan dengan bangun ruang dan statistika. Sebelum Gengs berlatih mengerjakan soal, ada baiknya pelajari dahulu materinya.
Tanpa berlama-lama lagi, berikut 10 soal matematika kelas 6 semester 2 disertai pembahasan.
Soal 1
Aku adalah bangun ruang. Aku memiliki 4 titik sudut dan 4 sisi. Aku juga memiliki 6 rusuk. Aku adalah bangun…
Pembahasan:
Diketahui: Suatu bangun ruang memiliki:
1) 4 titik sudut.
2) 4 sisi
3) 6 rusuk
Ditanya: Ketiga sifat tersebut dimiliki oleh bangun ruang ?
Perhatikan gambar berikut ini.

Gambar tersebut memiliki:
4 titik sudut yaitu A, B, C dan T.
4 sisi yaitu ABC, ABT, BCT dan ACT
6 rusuk yaitu AB, AC, BC, AT, BT dan CT
Dengan demikian, ketiga sifat tersebut dimiliki oleh bangun ruang limas segitiga.
Soal 2
Perhatikan gambar bangun ruang berikut.

Luas permukaan bangun ruang tersebut adalah… cm³.
Pembahasan:
Diketahui:
Panjang (p) = 26 cm
Lebar (l) = 15 cm
Tinggi (t) = 10 cm
Ditanya: Luas permukaan ?
Pertama-tama, kita harus tahu bangun ruang apakah gambar tersebut!
Bangun ruang tersebut adalah bangun ruang prisma segi empat karena memiliki 8 titik sudut, 12 rusuk dan 6 sisi.
Maka dengan mudah kita dapat menentukan luas permukaannya.
Luas permukaan = (p×l) + (l×t) + (p×t)
= (26×15) + (15×10) + (26×10)
= 390 + 150 + 260
=800 cm³
Jadi, luas permukaan bangun ruang tersebut adalah 800 cm³.
Soal 3
Perhatikan gambar bangun ruang berikut.
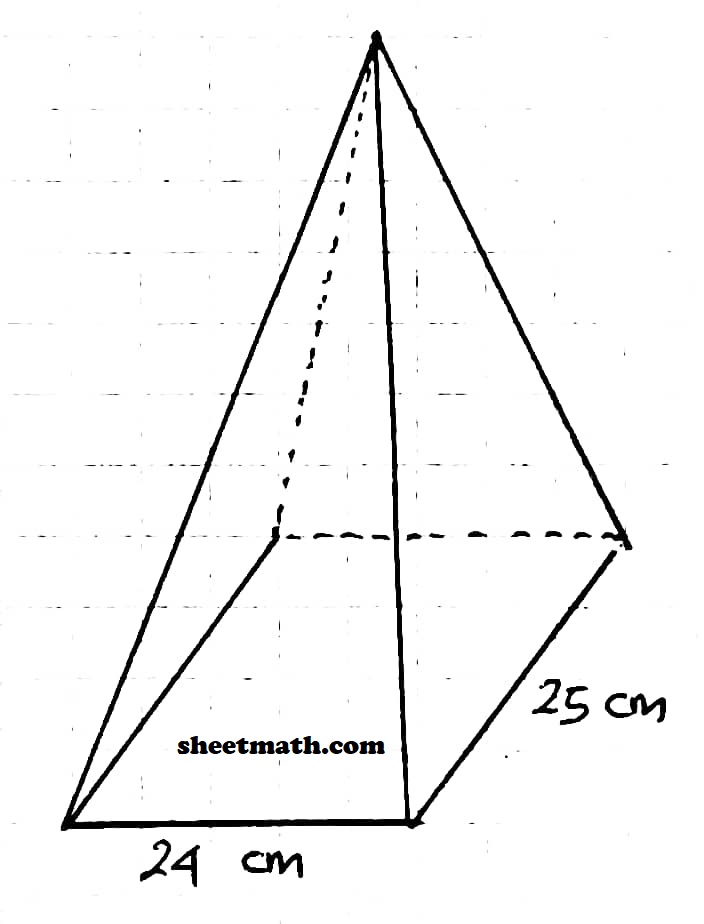
Jika volume limas tersebut 7.000 cm³, tinggi limas tersebut adalah… cm.
Pembahasan:
Diketahui:
Volume limas = 7000 cm³
Panjang (p) = 24 cm
Lebar (l) = 25 cm
Ditanya: Tinggi limas ?
Perlu kita tahu bahwa gambar tersebut adalah limas segi empat. Maka:
Volume limas = ⅓ × Luas alas × tinggi
Sebelum kita mencari tinggi, kita akan mencari luas terlebih dahulu.
Luas alas kita cari seperti mencari luas pada persegi dan persegi panjang yaitu panjang × lebar. Maka:
Luas alas = p × l
= 24 × 25
= 600 cm²
Dengan demikian,
Volume = ⅓ × Luas alas × tinggi
7000 = ⅓ × 600 × t
7000 = 200 × t
t = 7000/200 = 35 cm
Jadi, tinggi limas tersebut adalah 35 cm.
Soal 4
Perhatikan gambar bangun ruang gabungan berikut.
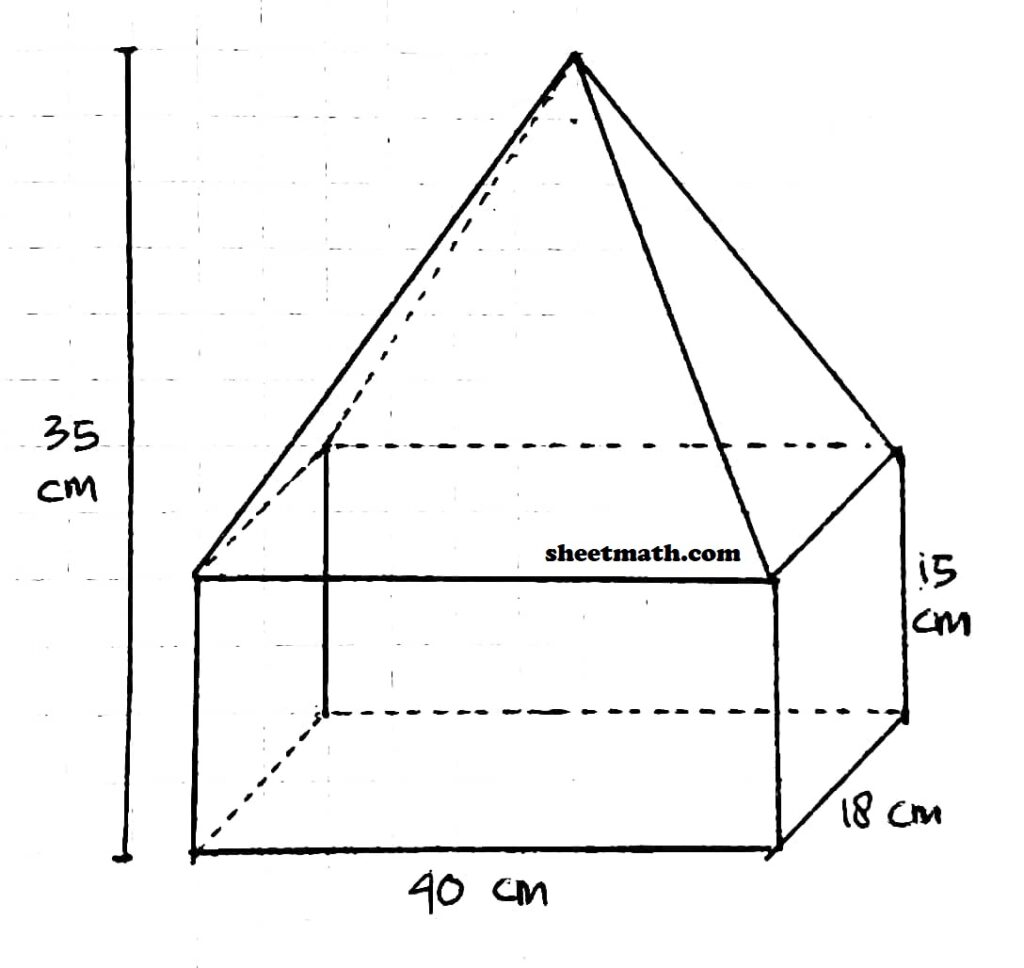
Volume bangun ruang gabungan di atas adalah… cm³.
Pembahasan:
Diketahui:
Panjang (p) = 40 cm
Lebar (l) = 18 cm
Tinggi pada prisma segi empat = 15 cm
Tinggi prisma segi empat dan limas segi empat (gabungan) = 35 cm
Ditanya: Volume bangun ruang gabungan (prisma segi empat dan limas segi empat).
Kita misalkan:
Volume limas segi empat = Vl
Volume prisma segi empat = Vp
Pertama, kita hitung volume prisma segi empat.
Vp = Luas alas × tinggi
= (p × l) × t
= (40 × 18) × 15
= 720 × 15
= 10800 cm³
Kedua, kita hitung volume limas segi empat.
Vl = ⅓ × luas alas × tinggi
Tinggi prisma segi empat = 15 cm
Tinggi prisma segi empat dan limas segi empat = 35 cm
Maka, tinggi limas segi empat = 35 – 15 = 20 cm
Vl = ⅓ × (p × l) × t
= ⅓ × (40 × 18) × 20
= ⅓ × 720 × 20
= 240 × 20
= 4800 cm³
Dengan demikian
Volume gabungan = Volume prisma segi empat + Volume limas segi empat
= 10800 + 4800
= 15600 cm³
Soal 5
Perhatikan gambar bangun ruang berikut ini.

Luas permukaan bangun ruang gabungan di atas adalah … cm³
Pembahasan:
Pada soal sebelumnya kita mengerjakan bangun ruang prisma dan limas. Pada soal ini kita akan mengerjakan bangun ruang prisma segi empat dan prisma segi empat.
Diketahui:
Kita misalkan prisma segi empat yang besar dengan A dan yang kecil dengan B. Sehingga,
Panjang_A (P_A) = 36
Lebar_A (l_A) = 12
Tinggi_A (t_A) = 14
Panjang_B (P_B) = 26
Lebar_B (l_B) = Lebar_A (l_A) = 12
Tinggi_B (t_B) = 7
Ditanya: Luas permukaan gabungan ?
Pertama, kita cari luas permukaan A.
Luas permukaan = (p × l) + (l × t) + (p × t)
= (36 × 12) + (12 × 14) + (36 × 14)
= 432 + 168 + 504
= 1104
Kedua, kita cari luas permukaan B
Luas permukaan = (p × l) + (l × t) + (p × t)
= (26 × 12) + (12 × 7) + (26 × 7)
= 312 + 84 + 182
= 578
Dengan demikian,
Luas permukaan gabungan = Luas permukaan A + Luas permukaan B
= 1104 + 578
= 1156 cm²
Soal 6
Perhatikan data berikut ini.
16, 20, 24, Δ, 25, 26
Median data tersebut 24,5. Nilai Δ adalah…
Pembahasan:
Median disebut juga nilai tengah. Untuk mencari median syaratnya data harus terurut dari data terkecil hingga terbesar. Pada soal ini nilai mediannya telah diketahui.
Pada soal ini, kita tidak dapat mengatakan bahwa data nya telah terurut karena ada satu data yang belum diketahui.
Langkah awal yang bisa kita lakukan yaitu mencari data yang belum diketahui tersebut menggunakan informasi yang diberikan pada soal.
Jika banyak datanya ganjil maka mediannya yaitu data yang berada di tengah atau jika dengan rumus:
Median = (n + 1)/2
Jika banyak datanya genap maka mediannya yaitu dua data yang berada di tengah kita jumlahkan lalu dibagi 2 atau jika dengan rumus:
Median = [data ke n/2 + data ke (n/2 + 1)]/2
Pada soal ini, banyal datanya genap maka kita akan menjumlahkan dua data ditengan lalu di bagi 2 atau jika dengan rumus akan seperti berikut.
Median = [data ke n/2 + data ke (n/2 + 1)]/2
24,5 = [data ke 6/2 + data ke 6/2 + 1]/2
24,5 = [data ke 3 + data ke 4]/2
24,5 = [24 + Δ]/2
24,5 × 2 = 24 + Δ
49 = 24 + Δ
Δ = 49 – 24 = 25
Soal 7
Mean dari data 85, 87, 88, 86, 87, 86, 87, 85, 88, 86 adalah…
Pembahasan:
Diketahui data berikut:
85, 87, 88, 86, 87, 86, 87, 85, 88, 86
Ditanya: Mean?
Mean disebut juga rata-rata.
Untuk mencari mean, kita tidak perlu mengurutkan datanya, kita hanya perlu mengetahui jumlah data dan banyak data. Maka,
Mean = Jumlah data / Banyak data
= (85 + 87 + … + 88 + 86) /10
= 865/10
= 86,5
Jadi, mean dari data tersebut adalah 86,5.
Soal 8
Tinggi badan (dalam cm) sebelas pemain sepak bola sebagai berikut.
172, 165, 170, 167, 162, 174, 171, 168, 170, 164, 165
Median dari data tersebut adalah… cm.
Pembahasan:
Diketahui data tinggi badan yaitu:
172, 165, 170, 167, 162, 174, 171, 168, 170, 164, 165
Ditanya: Median?
Median yaitu data yang berada ditengah.
Data pada soal ini belum diurutkan dari yang terkecil hingga terbesar maka akan kita urutkan terlebih dahulu.
162, 164, 165, 165, 167, 168, 170, 170, 171, 172, 174
Setelah diurutkan kita kan dengan mudah mencari mediannya menggunakan rumus.
Banyak data (n) yaitu 11 (ganjil) maka jika menggunakan rumus:
Median = data ke (n+1)/2
= data ke (11+1)/2
= data ke 6
= 168
Jadi, median dari data tersebut adalah 168 cm
Soal 9
Perhatikan tabel nilai ulangan siswa kelas VI berikut ini.
| Nilai Siswa | Banyak Siswa |
| 50 | 1 |
| 60 | 4 |
| 70 | 5 |
| 80 | 7 |
| 90 | 2 |
| 100 | 1 |
Siswa yang mendapat nilai di bawah rata-rata sebanyak… anak.
Pembahasan:
Untuk menjawab soal ini, kita harus mencari rata-rata nya (mean) terlebih dahulu.
Mean = Jumlah data / Banyak data
= [(50×1)+(60×4)+…+(100×1)]/(1+4+…+1)
= [50 + 40 + …+ 100] / 20
= 1480/20
= 74
Rata-rata nilai ulangan yaitu 74. Dengan demikian siswa yang mendapat nilai dibawah rata-rata sebanyak:
1) Nilai 70 ada 5 anak
2) Nilai 60 ada 4 anak
3) Nilai 50 ada 1 anak
Jadi, banyak anak yang mendapat nilai dibawah rata-rata yaitu 10 anak.
Soal 10
Perhatikan diagram batang yang menunjukkan data hasil penjualan lampu di Toko Cahaya selama 4 minggu sebagai berikut.

Rata-rata hasil penjualan lampu tiap minggu adalah… lampu.
Pembahasan:
Diketahui:
Minggu ke-1 = 30 lampu
Minggu ke-2 = 40 lampu
Minggu ke-3 = 25 lampu
Minggu ke-4 = 45 lampu
Ditanya rata-rata penjualan?
Rata-rata =( 30 + 40 + 25 + 45) / 4
= 140/4
= 35 lampu
Demikian 10 soal matematika kelas 6 semester 2 beserta pembahasan. Semoga bermanfaat.
2 komentar di “10 Soal Matematika Kelas 6 Semester 2 Disertai Pembahasan”