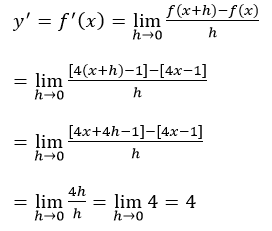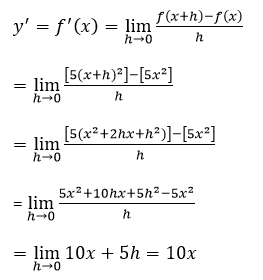Hi Gengs pada kesempatan kali ini saya akan berikan beberapa contoh tentang turunan fungsi. Sebelum kita berlatih kerjakan soal, saya akan memberikan sedikit ulasan tentang pengertian turunan pada suatu fungsi. Tanpa basa-basi lagi, mari kita bahas tuntas.
Apa itu definisi dari Turunan?
Misalkan kita diberi suatu fungsi katakan fungsi y=f(x), fungsi tersebut mempunyai turunan yang dinotasikan y’=f'(x) dan didefinisikan sebagai berikut:
Berikut ini contoh soal mencari turunan dengan menggunakan definisi turunan.
SOAL
Tentukan turunan dari f(x)=4x-1
Jawab:
untuk menjawab soal ini, mari kita mengacu pada definisi turunan di atas.
f(x)=4x-1
f(x+h)=4(x+h)-1
Berikut langkah-langkah pengerjaannya:
Tentukan turunan dari f(x)=5x²
Jawab
f(x)=5x²
f(x+h)=5(x+h)²
Berikut cara kerjanya
Dengan definisi turunan, tentukan turunan dari y=5x² + 2x
Jawab
y=f(x)=5x² + 2x
f(x+h)=5(x+h)² + 2 (x+h)
Berikut langkah-langkah pengerjaannya!
Apabila kita mencari turunan dari suatu fungsi menggunakan definisi turunan maka kita harus yakin bila limitnya ada dan bukan ∞ atau -∞.Dari ketiga contoh di atas, sebenarnya kita dapat mengetahui hasil turunannya tanpa menggunakan definisi dari turunan, yaitu dengan mengetahui aturan-aturan pencarian turunan diantaranya aturan fungsi konstanta, aturan fungsi satuan, aturan pangkat dan aturan kelipatan konstanta.
Misal:f(x)=4x-1, dengan aturan kelipatan konstanta dan aturan fungsi konstanta kita akan lebih mudah mendapat hasinya
ATURAN FUNGSI KONSTANTA
Jika f(x)=k,dengan k suatu konstanta maka untuk sebarang x, f'(x)=0
ATURAN FUNGSI KONSTANTA
Jika f(x)=x maka f'(x)=1
ATURAN PANGKAT
Jika f(x)=xⁿ, dengan n bilangan bulat positif, maka f'(x)=nxⁿ-1
ATURAN KELIPATAN KONSTANTA
Jika k suatu konstanta dan f suatu fungsi yang terdiferensialkan, maka (k.f)(x)=k.f'(x)SOAL
Tentukan turunan dari f(x)=(x³ + 2x² -3x)⁶⁰
Jawab
kita bisa menggunakan definisi untuk menjawab soal tersebut, tetapi akan sangat rumit karena kita harus memperkalikan 60 faktor kuadrat dari x³ + 2x² -3x kemudian mendiferensialkan fungsi polinom yang dihasilkan. Oleh karena itu dikenal ATURAN RANTAI untuk menjawab soal seperti di atas.Apa itu aturan rantai?
Misalkan y=f(u) dan u=g(x). Jika g terdiferensiasikan di x dan f terdiferensiasikan di u=g(x), maka fingsi komposit fₒg, yang didefinisikan oleh (fₒg)(x)=f(g(x)), adalah terdiferensiasikan di x dan
(fₒg)'(x)=f'(g(x))g'(x) yakni Dₓ(f(g(x))=f'(g(x))g'(x) atau dy/dx = dy/du du/dy
Dengan menggunakan aturan rantai, akan kita peroleh sebagai berikut:
Misalkan y=f(u)=u⁶⁰ dan u=g(x)=x³ + 2x² – 3x
Maka
Dₓy=Dₓf(g(x))
=f'(g(x))g'(x)
=f'(u)g'(x)
=60u⁵⁹ (3x² + 4x – 3)
=60(x³ + 2x² – 3x)⁵⁹ (3x² + 4x – 3)
SOAL
Jika y=1/(2x⁵ – 7)³, carilah Dₓy
Jawab
Misalkan y=f(u)=1/u³=u^⁻³ dan u=g(x)=2x⁵ – 7
Maka
Dₓy=Dₓf(g(x))
=f'(g(x))g'(x)
=f'(u)g'(x)
=-3u⁻⁴(10x⁴)
=-30u⁻⁴x⁴
=-30(2x⁵ – 7)⁻⁴x⁴
=-30x⁴/(2x⁵ – 7)⁴
SOAL
Jika y=√(4x+5), tentukan dy/dx!
Jawab
Misal:
y=f(u)=√u maka dy/du=1/2 √u
u=4x+5 maka du/dx=4
Dengan demikian
dy/dx = dy/du du/dx
d√(4x+5)/dx = [1/2√u] [4] = 4/2√u = 2/√(4x+5)
Baca Juga: Turunan – Aturan Rantai, Turunan Implisit, Turunan Tingkat Tinggi dan Laju Terkait
Bagaimana jika fungsi berbentuk implisit.
Fungsi implisit yaitu fungsi yang terdiri dari variabel bebas dan variabel tak bebas yang berada dalam satu ruas dan tidak dapat dipisahkan pada ruas yang berbeda.
Contoh fungsi implisit: y⁴ – x⁴ – 6y²x³=0
Berikut diberikan dua contoh soal apabila fungsinya berbentuk implisit.
SOAL
Tentukan dy/dx dari 3x³ + 4y³ + 8=0
Jawab
d/dx (3x³ + 4y³ + 8)= d/dx(0)
9x² + 12y² dy/dx = 0
12y² dy/dx = -9x²
dy/dx = -9x²/12y²
Baca Juga: Rangkuman, Contoh Soal dan Pembahasan – Turunan Implisit
SOAL
Tentukan dy/dx dari sin(xy²) + 4x = y³
Jawab
d/dx [sin(xy²) + 4x] = d/dx [y³]
d/dx [sin(xy²)] + d/dx 4x = d/dx [y³]
cos(xy²)[y² + 2xy dy/dx] + 4 = 3y² dy/dx
y² cos(xy²) + 2xy cos(xy²) dy/dx + 4 = 3y² dy/dx
2xy cos(xy²) dy/dx – 3y² dy/dx = y² cos(xy²) – 4
[2xy cos(xy²) – 3y²] dy/dx = y² cos(xy²) – 4
dy/dx = [y² cos(xy²) – 4]/[2xy cos(xy²) – 3y²]
