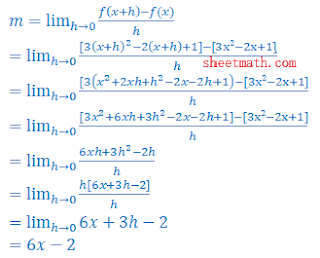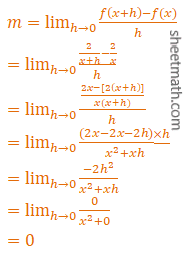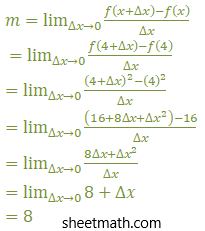Soal 1
Dengan menggunakan konsep limit fungsi, tentukan gradien garis singgung fungsi f(x)=3x²-2x+1.
Penyelesaian:
Dengan menggunakan konsep limit fungsi, berikut gradien garis singgungnya.
Dengan menggunakan konsep limit fungsi, tentukan gradien garis singgung fungsi f(x)=2/x.
Rumus yang digunakan untuk menghitung gradiennya sebagai berikut.
Soal 3
Tentukan persamaan garis singgung di titik dengan absis x=4 pada kurva f(x)=x².
Penyelesaian:
Diketahui
x₁=4
y₁=x²=4²=16
dengan demikian titik singgungnya adalah (x₁,y₁)=(4,16)
Ditanya: persamaan garis singgung??
Untuk memperoleh persamaan garis singgung, pertama-tama kita cari gradient garis singgungnya.
Rumus yang digunakan untuk menghitung gradiennya sebagai berikut.
y₂-y₁=m(x₂-x₁)
y₂-16=8(x₂-4)
y₂-16=8x₂-32
y₂-8x₂+16=0
Tentukan persamaan garis singgung dan persamaan garis normal di titik dengan absis x=1 pada kurva f(x)=2/x².
Penyelesaian
Diketahui:
x₁=1
y₁=2/x²=1/1²=1
dengan demikian titik singgungnya adalah (x₁,y₁)=(1,1)
Ditanya: persamaan garis singgung dan persamaan garis normal ?
Untuk memperoleh persamaan garis singgung, pertama-tama kita cari gradient garis singgungnya.
Rumus yang digunakan untuk menghitung gradiennya sebagai berikut.
y₂-y₁=m(x₂-x₁)
y₂-1=2(x₂-1)
y₂-1=2x₂-2
y₂-2x₂+1=0
Sedangkan persamaan garis normalnya adalah:
y₂-y₁=-1/m(x₂-x₁)
y₂-1=-1/2(x₂-1)
y₂-1=-1/2x₂+1/2
y₂-(1/2)x₂-3/2=0
Tentukan persamaan garis singgung kurva y=f(x)=(x+2)⁻⁹ di titik (-1,1).
Penyelesaian
Langkah 1. Menentukan titik singgung
Misalkan x₁=-1 dan y₁=1
Karena f(-1)=(-1+2)⁻⁹=1 maka titik (-1,1) berada pada kurva.
Langkah 2. Mencari gradient garis singgung
Cari dahulu turunan pertamanya di fungsi tersebut.
f(x)=(x+2)⁻⁹
f’(x)=(-9)(x+2)⁻¹⁰
Langkah 3. Menentukan persamaan garis singgung
Diketahui gradient garis singgung di titik (-1,1) maka
f’(x)=(-9)(x+2)⁻¹⁰
f’(-1)=(-9)(-1+2)⁻¹⁰=-9
Dengan demikian, persamaan garis singgungnya adalah..
y-y₁ = m(x-x₁)
y-1=-9(x-(-1))
y-1=-9(x+1)
y-1=-9x-9
y+9x+8=0
Tentukan persamaan garis singgung kurva y=f(x)= √(2x²+1) di titik (-2,3).
Penyelesaian
Langkah 1. Menentukan titik singgung
Misalkan x₁=-2 dan y₁=3
Karena f(-2)=√(2.(-2)²+1)=√9=3 maka titik (-2,3) berada pada kurva.
Langkah 2. Mencari gradien garis singgung
Cari dahulu turunan pertamanya di fungsi tersebut.
f(x)= √(2x²+1)
f(x)= \((2x²+1)^½\)
f’(x)=(½)(4x)\((2x²+1)⁻^½\)
Langkah 3. Menentukan persamaan garis singgung
Diketahui gradient garis singgung di titik (-2,3) maka
f’(x)=(½)(4x)\((2x²+1)⁻^½\)
=(2x)\((2x²+1)⁻^½\)
f’(-2)=(2(-2)) \((2(-2)²+1)⁻^½\)
=(-4) \((9)⁻^½\)
=(-4)(⅓)
=-4/3
Dengan demikian, persamaan garis singgungnya adalah..
y-y₁ = m(x-x₁)
y-3=-4/3(x-(-2))
y-3=-4/3(x+2)
y-3=(-4/3)x-(8/3)
3y-9=-4x-8
3y+4x-1=0
Soal 7
Dengan konsep turunan, tentukan turunan pertama dari fungsi f(x)=x⁻³
Penyelesaian
f(x)=x⁻³
f’(x)=(-3)x⁻³⁻¹=(-3)x⁻⁴
Soal 8
Dengan konsep turunan, tentukan turunan pertama dari fungsi f(x)=(3x-2)⁻²
Penyelesaian
Misalkan u(x)=3x-2 sehingga u’(x)=3
Dengan demikian,
f(x)=(3x-2)⁻² menjadi (u(x))⁻² sehingga
f’(x)=(-2)(u(x))⁻²⁻¹ u’(x)
f’(x)=(-2)(3x-2)⁻²⁻¹ (3) = (-6)(3x-2)⁻³
Dengan konsep turunan, tentukan turunan pertama dari fungsi f(x)=x²(2x+1)⁵
Penyelesaian
Misalkan:
u(x)=x² sehingga u’(x)=2x
v(x)= (2x+1)⁵ sehingga v’(x)=5(2x+1)⁴(2)=10(2x+1)⁴
Dengan demikian,
f’(x)=u’(x)v(x) + u(x)v’(x)
=(2x)((2x+1)⁵) + x² (10(2x+1)⁴)
=2x (2x+1)⁵ + 10x² (2x+1)⁴
=(2x+1)⁴ (2x(2x+1) + 10x²)
=(2x+1)⁴ (4x²+2x) + 10x²)
Dengan konsep turunan, tentukan turunan pertama dari fungsi f(x)=(2x-1)/(x+1)
Penyelesaian
Misalkan:
u(x)=2x-1 maka u’(x)=2
v(x)=x+1 maka v’(x)=1
Dengan demikian,
f'(x)=(u'(x)v(x)-u(x) v^(x))/(v(x))^2
=(2(x+1)-(2x-1)(1))/(x+1)^2
=(2x+2-2x+1)/(x+1)^2
=3/((x+1)²)
Dengan konsep turunan, tentukan turunan pertama dari fungsi f(x)=2x²(-3x+1)⁵
Penyelesaian
Misalkan
u(x)=2x² maka u’(x)=4x
v(x)=(-3x+1)⁵ maka v’(x)=(5)(-3)(-3x+1)⁴=-15(-3x+1)⁴
f’(x)=u’(x)v(x) + u(x)v’(x)
= (4x) (-3x+1)⁵ + 2x² ( -15(-3x+1)⁴)
= (4x) (-3x+1)⁵ – (30x²)(-3x+1)⁴
Tentukan turunan kedua dari fungsi f(x)=(3x⁴-2)²
Penyelesaian
f(x)=(3x⁴-2)²
f’(x)=(2)(12x³)(3x⁴-2)
=(24x³)(3x⁴-2)
=72x⁷-48x³
f’’(x)=(72)(7)x⁶ – (48)(3)x²
=154x⁶ – 144x²
Tentukan turunan kedua dari fungsi f(x)=(2x)/(x+1)
Penyelesaian
f(x)=(2x)/(x+1)
misalkan
u(x)=2x maka u’(x)=2
v(x)=x+1 maka v’(x)=1
Dengan demikian,
f'(x)=(u'(x)v(x)-u(x) v'(x))/(v(x)²)
=(2x+2-2x)/(x+1)²
=2/((x+1)²)
f’’(x)=2(x+1)⁻²=(2)(-2)(x+1)⁻³ =(-4)(x+1)⁻³
Tentukan titik balik fungsi f(x)=x²-2x
Penyelesaian
Pada penyelesaian bagian 1 ini kita akan kerjakan berdasarkan konsep fungsi turunan.
f(x)=ax²+bx+c mempunyai titik balik (-b/2a , -D/4a) dimana fungsi mencapai maksimum untuk a<0 dan mencapai minimum untuk a>0.
Jawab:
f(x)=x²-2x dengan:
a=1,
b=-2,
c=0,
D= b²-4ac=(-2)²-4(1)(0)=4
Titik balik dari fungsi f(x)=x²-2x adalah (-(-2)/2(1) , (-4)/4(1))=(2/2 , -4/4)=(1,-1)
Pada fungsi f(x)=x²-2x, a>0 maka titik balik fungsi tersebut adalah minimum di (1,-1)
Tentukan titik balik fungsi f(x)=x³-6x²-9x+1
Penyelesaian
Pada soal ini kita akan kerjakan dengan konsep turunan.
Berikut penyelesaiannya:
Pertama-tama kita cari titik stasionernya.
Fungsi f(x)=x³-6x²+9x+1
f’(x)=3x²-12x+9
=3(x-3)(x-1)
x=3 dan x=1
Kemudian, untuk menentukan titik balik maksimum atau minimum fungsi, akan kita uji titik stasioner pada turunan kedua fungsi.
f(x)=x³-6x²+9x+1
f’(x)=3x²-12x+9
f’’(x)=6x-12
x=3 maka f’’(x)=6(3)-12=18-12=6>0
x=1 maka f’’(x)=6(1)-12=-6<0
Titik (3,6) adalah titik balik minimum
Titik (1,-6) adalah titik balik maksimum
Tentukan titik balik fungsi f(x)=x⁴-x²
Penyelesaian
Pertama mari kita tentukan titik stasioner.
f(x)=x⁴-x²
f’(x)=4x³-2x=0
2x(x²-1)=0
x=0 atau x=1 atau x=-1
Untuk menentukan titik balik maksimum atau minimum fungsi, akan kita uji ttitk stasionernya kedalam turunan kedua fungsi tersebut dengan cara berikut.
f(x)=x⁴-x²
f’(x)=4x³-2x
f’’(x)=12x²-2
f’’(x)=12x²-2
untuk x=0
f’’(0)=12(0²)-2=-2<0
untuk x=1
f’’(1)=12(1²)-2=10>0
untuk x=-1
f’’(-1)=12(-1²)-2=10
Titik (0,-2) merupakan titik balik maksimum
Titik (-1,10) merupakan titik balik minimum
Tentukan titik belok fungsi f(x)=x²+3x
Penyelesian
f’(x)=2x+3
f’’(x)=2
Nilai f(2)=2²+3(2)=4+6=10
Jadi, nilai titik belok fungsi tersebut adalah (2,10)
Tentukan titik belok fungsi f(x)=x³-6x
Penyelesaian
f’(x)=3x²-6
f’’(x)=6x
Buat turunan keduanya sama dengan nol.
f’’(x)=0
6x=0
x=0
Nilai f(0)=0³-6(0)=0
Jadi, nilai titik belok fungsi tersebut adalah (0,0)
Tentukan titik belok fungsi x⁴-4x²
Penyelesaian
f’(x)=4x³-8x
f’’(x)=12x²-8
Kita buat fungsi turunan keduanya sama dengan nol.
f’’(x)=0
12x²-8=0
12x²=8
x²=⅔
x=√⅔
nilai f(√⅔)=(√⅔)⁴- 4(√⅔)² = 4/9 – 8/3 = -20/9
Jadi, titik beloknya adalah (√⅔ , -20/9)